Relaciones y funciones |
Entender los conceptos de Relación y de Función es de suma importancia en Matemática.
Para lograr esa comprensión es necesario adentrarnos en la noción de Correspondencia , ya que esta tiene un papel fundamental en las relaciones y funciones.
Lo primero es entender que Correspondencia es equivalente a Relación . En nuestra lengua, decir “en relación a”, es equivalente a decir “corresponde a”.
Ejemplos:
En una tienda comercial, cada artículo está relacionado con su precio; o sea, a cada artículo le corresponde un precio.
En la guía telefónica, cada cliente está relacionado con un número; o sea, a cada nombre de la guía le corresponde un número.
Definición matemática de Relación y de Función
En matemática,
Relación
es la correspondencia de un primer conjunto, llamado
Dominio
, con un segundo conjunto, llamado
Recorrido o Rango
, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Por su parte, una
Función
es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde
uno y sólo un valor
del Recorrido.
De las definiciones anteriores podemos deducir que todas las funciones son relaciones , pero no todas las relaciones son funciones.
También debemos agregar que toda ecuación es una Relación , pero no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.
Ver: Plano Cartesiano
Dados dos conjuntos A y B una relación definida de A en B es un conjunto de parejas ordenadas ( par ordenado ) que hacen verdadera una proposición; dicho de otro modo, una relación es cualquier subconjunto del producto cartesiano A x B
Ejemplo 1.
Si A = {2, 3} y B = {1, 4, 5}, encontrar tres relaciones definidas de A en B.
Solución
El producto cartesiano de A x B está conformado por las siguientes parejas o pares ordenados:
A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y cada uno de los siguientes conjuntos corresponde a relaciones definidas de A en B:
R1 = {(2, 1), (3, 1)}
R2 = {(2, 4), (2, 5), (3, 4), (3, 5)}
R3 = {(2, 4), (3, 5)}
La relación R1 se puede definir como el conjunto de pares cuyo segundo elemento es 1, esto es, R1 = {( x , y ) / y = 1}.
La relación R2 está formada por los pares cuyo primer componente es menor que el segundo componente, R2 = {( x , y ) / x < y }
Y la relación R3 está conformada por todos los pares que cumplen con que el segundo componente es dos unidades mayor que el primer componente, dicho de otro modo, R3 = {( x , y ) / y = x + 2}
Así, se puede continuar enumerando relaciones definidas a partir de A x B. Como se puede ver, la regla que define la relación se puede escribir mediante ecuaciones o desigualdades que relacionan los valores de x e y . Estas reglas son un medio conveniente para ordenar en pares los elementos de los dos conjuntos.
Ejemplo 2.
Dados los conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares ordenados ( x , y ) que satisfagan la relación
R = {( x , y ) / x + y = 3}
Solución
El producto cartesiano de C x D está formado por los siguientes pares ordenados
C x D = {(1, 2), (1, 3), (1, 6), (–3, 2), (–3, 3), (–3, 6)}
Las parejas ordenadas que satisfacen que la suma de sus componentes sea igual a 3 son:
R = {(1, 2), (–3, 6)}
Toda relación queda definida si se conoce el conjunto de partida, el conjunto de llegada y la regla mediante la cual se asocian los elementos. En el ejemplo anterior, el conjunto de partida corresponde al conjunto C , el conjunto de llegada es el conjunto D y la expresión x + y = 3 es la regla que asocia los elementos de los dos conjuntos.
Dominio y rango de una relación
El dominio de una relación es el conjunto de preimágenes ; es decir, el conjunto formado por los elementos del conjunto de partida que están relacionados. Al conjunto de imágenes , esto es, elementos del conjunto de llegada que están relacionados, se le denomina recorrido o rango .
Ejemplo 3
Sea A = {1, 2, 3, 4} y B = {4, 5, 6, 7, 8} y R la relación definida de A en B determinada por la regla “ y es el doble de x ” o “ y = 2 x ”, encontrar dominio y rango de la relación.
Solución
El total de pares ordenados que podemos formar, o producto cartesiano es:
A x B = {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R (y = 2x) son solo:
R = {(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: “4 es el doble de 2”; esto es, “4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”.
Así, el dominio y rango son:
D = {2, 3, 4}
Rg = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de partida?
En el Dominio falta el elemento 1 del conjunto de partida, por lo tanto el Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de llegada es elemento del rango?
La respuesta es no, pues en el rango faltan el 5 y el 7.
Representación gráfica de las relaciones
Los pares ordenados se pueden representar gráficamente por medio de diagramas sagitales o por medio de puntos en el plano cartesiano . Veamos el siguiente ejemplo.
Ejemplo 4
Si A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y R la relación definida por la regla
R = {( x , y ) / y = 2 x + 1}, graficar R.
Solución
Los pares ordenados que pertenecen a la relación (que cumplen con y = 2x + 1) son:
R = {(1, 3), (2, 5), (3, 7), (4, 9)}
Y la gráfica correspondiente es la siguiente:
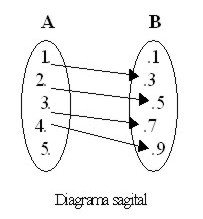
|
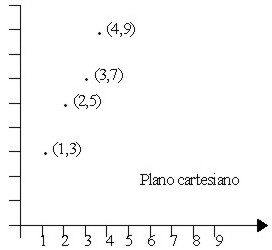
|
Fuente Internet:
http://netlizama.usach.cl/avcapituloII.pdf

