Multiplicación de raíces |
Multiplicación de raíces de igual índice
Según una propiedad de los radicales:
Esto significa que si dos números están multiplicándose dentro de una raíz, se puede extraer la raíz de cada uno de ellos en forma separada y luego multiplicarlos; o también que si hay dos raíces de igual grado multiplicándose se pueden multiplicar los números y obtener la raíz después.
Ejemplo 1:
Dentro de la raíz cuadrada tenemos una multiplicación (9x4), sacamos la raíz cuadrada a cada uno de los números para finalmente multiplicarlos.
Ejemplo 2:
En este ejemplo, igual anotamos el radical en forma separada, pero como no es posible extraer la raíz exacta a ninguno de los nuevos radicales, lo más conveniente es multiplicar las bases (12 x 3) primero y luego sacar la raíz cuadrada al resultado.
Veamos otros ejemplos a modo de práctica:
Ejemplo 3:
Calcular el producto de
En este caso vemos que aparecen números fuera del signo radical (fuera de la raíz), entonces, lo primero que hacemos es multiplicar las cantidades que están fuera de las raíces (5 x 3) ya que todas tienen el mismo índice. Luego multiplicamos las cantidades bases (subradicales o radicandos, como quieran llamarlas) (18 x 8 = 144), y si se puede extraemos el valor de la raíz
para colocarlo, multiplicando (15 x 12), fuera del signo radical.
Ejemplo 4:
Calcular el producto de
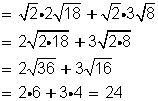
Para multiplicar un número por una suma, se multiplica cada sumando por ese número.
En este caso, multiplicamos
por cada número que se halla dentro del paréntesis. Dejamos la misma raíz y multiplicamos las bases o radicandos. Después, extraemos las raíces que podamos.
Ejemplo 5:
Calculemos
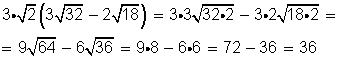
Para tener en cuenta:
Al multiplicar lo que está fuera del paréntesis por cada término dentro de él, tenemos que tener en cuenta que si hay números fuera de las raíces los multiplicamos lo mismo que los radicandos.
Nota Importante:
No debemos olvidar que solo podemos sacar fuera de las raíces números que estén dividiendo o multiplicando. Si los números suman o restan no pueden sacarse fuera del símbolo radical.
Por ejemplo: Para calcular
no debemos encontrar la raíz cuadrada de 16 y luego la raíz cuadrada de 4 para sumarlas, no está permitido. En este caso, como es una suma, debemos obligadamente ejecutar la suma y en este resultado extraer la raíz cuadrada (si es posible hacerlo).
Entonces:
Multiplicación de raíces de distinto índice
Para realizar una multiplicación de radicales que tengan distinto índice es obligatorio reducir esos índices distintos a un índice común (igual para todos los radicales).
Reducción de radicales a índice común
¿Cómo hacerlo?
El primer paso es hallar el mínimo común múltiplo (m.c.m.) de los índices , que será el índice común.
Luego, dividimos ese índice común por cada uno de los índices y cada resultado obtenido se multiplica por sus exponentes correspondientes.
Veamos un ejemplo:
Si tuviésemos que multiplicar entre sí las cantidades siguientes:
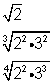
La primera raíz tiene índice 2; la segunda, 3, y la tercera, 4. Entonces tenemos que encontrar el m.c.m. entre 2, 3 y 4, que resulta ser 12. Dividimos 12 por cada índice y el resultado de cada división lo multiplicamos por cada uno de los exponentes de las cantidades bases o radicandos; de la siguiente manera:
12 ÷ 2 (2 es el índice de la primera raíz) = 6, este 6 lo multiplicamos por 1 (1 es el exponente) y nos queda
Después, 12 ÷ 3 (3 es el índice de la segunda raíz) = 4, este 4 lo multiplicamos por 2 en cada uno de los multiplicandos que hay dentro del raíz (ambos tiene exponente 2) y nos queda
En seguida, hacemos 12 ÷ 4 (4 es el índice de la tercera raíz) = 3, este 3 lo multiplicamos por 2 (exponente del primer multiplicando dentro de la raíz) y por 3 (exponente del segundo multiplicando dentro de la raíz) y nos queda
Ahora podemos hacer la operación, teniendo tres raíces con igual índice (12):
Veamos otro ejemplo:
Si tenemos
el m.c.m. entre 2, 3 y 4 es 12
Entonces:
Otro ejemplo:
m.c.m.
de 2 y 3 es = 6, que se convierte en el índice común.
Hacemos 6 ÷ 2 = 3 x 1 = 3, para que tengamos
Y hacemos 6 ÷ 3 = 2 x 1 = 2, para que tengamos
Y ahora tenemos:
Nótese que después de llevar las raíces a un índice común (6), factorizamos las bases o radicandos (12 = 2 2 x 3) y (36 = 2 2 x 3 2 ) y para llegar al resultado final sacamos afuera del signo radical un 2 (obtenido de 2 10 y dejando 2 4 dentro del signo radical), y un 3 (obtenido de 3 7 y dejando 3 dentro del signo radical).
Ejercicios de multiplicación de radicales
Ejercicio 1)
Ejercicio 2)
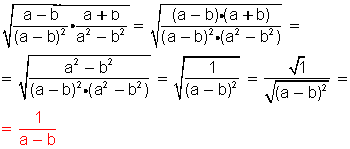
Ver: PSU: Matemáticas,
Pregunta 19_2010
Fuentes Internet:
http://www.aulafacil.com/matematicas-potencias-raices/curso/Lecc-11.htm
http://www.aulafacil.com/matematicas-potencias-raices/curso/Lecc-9.htm
http://www.vitutor.net/2/4/5.html