El rectángulo áureo de Euclides |
Para entender de qué se trata este tema, veamos la figura siguiente:
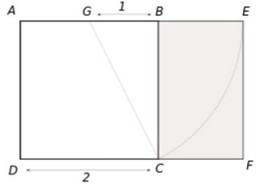
Como ya vimos lo que es la proporción áurea , visitemos a Euclides , el famoso matemático y geómetra griego, quien a partir del cuadrado ABCD (de la figura) obtiene geométricamente el rectángulo áureo AEFD . El rectángulo BEFC es, asimismo, áureo.
El rectángulo AEFD también es áureo porque sus lados AE y AD están en la proporción del número áureo. Euclides logra su construcción de este modo:
Se marca G en el centro del lado superior del cuadrado cuyo lado mide 2 (queda dividido en dos segmentos de valor 1 cada uno).
Con centro en G y radio GC se obtiene el punto E, y, por lo tanto:
![]() (valor de la hipotenusa del triángulo GBC, de lados 1 y 2)
(valor de la hipotenusa del triángulo GBC, de lados 1 y 2)
Ver: Raíz cuadrada de cinco
con lo que resulta evidente que
![]()
donde, finalmente, reemplazando llegamos a
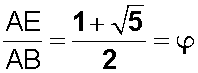
Por otra parte, los rectángulos AEFD y BEFC son semejantes , de modo que este último es asimismo un rectángulo áureo .
Ejemplo y comprobación matemática
Veamos ahora la comprobación u obtención matemática del valor del segmento desconocido, el cual nos hará cumplir con la proporción en el rectángulo:
Tenemos un cuadrado de 2 x 2 (ABCD arriba en la figura) y queremos obtener el rectángulo áureo a partir de este.
Tenemos la fórmula conocida de la proporción áurea:
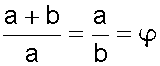
Recuerde que su valor es 1,618
Hacemos, entonces
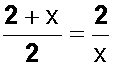
proporción áurea, donde x es el segmento desconocido (b) y 2 es el segmento conocido (a)
Resolvemos la ecuación
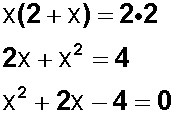
Tenemos una ecuación de segundo grado de la forma
ax 2 + bx – c = 0
donde a = 1
b = 2
c = —4 (como la fórmula es —c, el —4 queda positivo)
Sabemos que la fórmula para resolver una ecuación de este tipo es
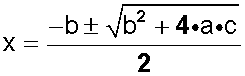
reemplazamos los valores que tenemos, y nos queda
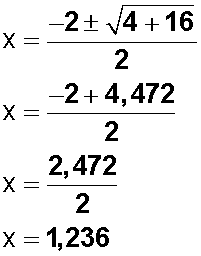
(Usamos la opción positiva (+), pues la opción negativa (-) no funciona)
Comprobación:
ABCD cuadrado de 2 x 2
Segmento AB = 2 (a)
Segmento BE = 1,236 (b)
Rectángulo AEFD = 2 x 3,236
Proporción áurea
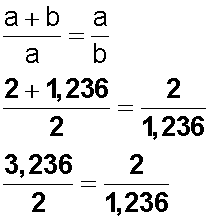
1,618 = 1,618
Respuesta: Un rectángulo de 3,236 x 2 está en proporción áurea a partir de un cuadrado de 2 x 2.
Nota: de este modo se puede calcular cualquier rectángulo en proporción áurea a partir de cualquier cuadrado.
Sobre la composición fotográfica y el número áureo, revisar la página
Ver, además:
http://matematicas.uclm.es/ita-cr/web_matematicas/trabajos/240/La_seccion_aurea_en%20arte.pdf
http://laproporcionperfecta.blogspot.cl/2011/06/numero-de-oro.html

