Máximo común divisor (M.C.D.) .

¿Qué significa esto?

Primero, debemos saber que todos los números pueden ser divididos por un divisor o por varios.

Por ejemplo, el 12 puede ser dividido por 2, por 3, por 4, por 6  y por 12; o sea, tiene 5 divisores, y de ellos el Máximo es el 12.

Otro número, el 18 puede ser dividido por 2, por 3, por 6, por 9 y por 18; o sea, tiene 5 divisores, y de ellos el Máximo es el 18.

Ahora, entre estos dos números, 12 y 18, hay tres divisores que son comunes (el 2, el 3 y el 6);  y de entre ellos, el mayor es el 6.

Entonces, el M.C.D. entre 12 y el 18 es el 6

De manera general, podemos decir que, si hay dos o más números dados o conocidos, el M C.D. es, de entre los varios divisores exactos comunes que haya para esos números, el mayor de esos divisores exactos.

Veamos la forma matemática de obtener el M.C.D. para cualquier conjunto igual o mayor a dos números.

Para su comprensión, veamos el ejemplo anterior:

Tenemos los números (dados o conocidos): 12 y 18.

Debemos encontrar el número mayor que los divida a ambos a la vez en forma exacta.
¿Cómo lo hacemos?

Hacemos la factorización prima de cada uno:

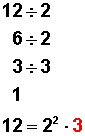
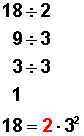
De entre todos los factores primos que obtuvimos, elegimos los factores comunes elevados al menor exponente:

En ambas factorizaciones se repiten los factores comunes 2 y 3, y marcados en rojo vemos que son los elevados al menor exponente (el exponente de ambos es 1).

Por lo tanto, los multiplicamos entre sí:  2 por 3 es igual a 6, entonces 6 es el M.C.D. entre 12 y 18.

Nótese que el 2 y el 3 también los pueden dividir a ambos en forma exacta, pero son menores que 6, Por ello, no pueden ser el Máximo Común Divisor (M.C.D.) de ambos.

Volver a: Números primos

Ver: Mínimo común múltiplo (m.c.m.)