Procesamiento de la información: tablas y gráficos |
Formas de recopilar, organizar, procesar e interpretar datos en tablas y gráficos
Recopilar y procesar datos se ha convertido en una necesidad imperiosa en la actualidad. Conocerlos e interpretarlos le permite al hombre de hoy descubrir, prevenir, informar o predecir el comportamiento de diferentes sucesos o fenómenos propios de la naturaleza, del entorno social o incluso del pensamiento.
En cualquier caso, disponer en una tabla los datos obtenidos nos facilitará su interpretación y su representación gráfica.
|
| Un gráfico permite visualizar datos complejos. |
¿Cómo recopilar los datos?
Hay varias formas: puede ser mediante la observación, mediante entrevistas, haciendo encuestas o consultando documentos.
Etapas para la recopilación y procesamiento de la información
Independientemente del sistema que usemos para recopilar datos, debemos seguir un esquema o pauta de trabajo que involucre:
Definición del problema :
Definir el fenómeno o proceso que queremos investigar. Por ejemplo, queremos saber cuántas personas conforman la familia de cada estudiante de secundaria en una cierta región del país.
Planificación:
Determinar cómo se van a obtener los datos y seleccionar la muestra dentro de la población.
En el caso de nuestro ejemplo, hacer una encuesta a todos los alumnos de las secundarias de la región sería una forma de encontrar los datos que nos piden (número de personas en la familia) pero requeriría mucho tiempo y sería algo costoso.
Por tal razón se puede seleccionar de forma adecuada una muestra y a ellos se les aplica la encuesta.
El total de alumnos de todas las escuelas secundarias de la región constituye la población .
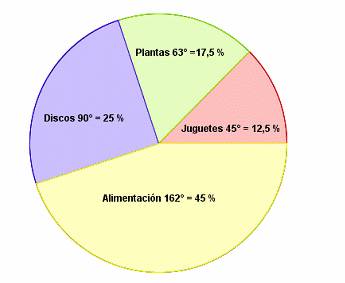
|
| Gráfico estadístico circular. |
La población es el conjunto fuente para conseguir la información requerida.
La muestra es el subconjunto finito de la población. Debe ser representativa de la característica que se desea estudiar.
Generalmente, el trabajo con muestras es más económico y más práctico, pero en el caso de los censos de Población y Vivienda es necesario trabajar con toda la población.
Recopilación datos :
Ejecución en terreno, se aplican las encuestas o las entrevistas para obtener los datos solicitados.
En el ejemplo, se pregunta a cada integrante de la muestra ¿Cuántas personas conforman su núcleo familiar?
Procesamiento de la información :
Esta fase consta de tres partes.
Organización de los datos: Se ordena la información
Presentación de los datos: Puede hacerse mediante tablas o gráficos.
Análisis e interpretación de los datos: Esdonde se llega a conclusiones sobre la investigación y con los resultados se pueden realizar pronósticos, hacer valoraciones y tomar decisiones.
Construcción de Tablas de valores
Dependiendo de la modalidad de trabajo, el conjunto de datos recopilados podemos tenerlos como una expresión verbal, como una fórmula o una ecuación.
Veamos un ejemplo de como construir una tabla de doble entrada cuando obtenemos los datos de forma verbal o mediante una ecuación.
Datos en forma verbal:
El club deportivo de mi ciudad cuenta con 2.000 socios. De ellos 200 practican natación, 350 practican fútbol, 150 practican voleibol, 400 practican baloncesto, 300 practican atletismo, 100 practican tenis, 240 practican
balonmano y 260 practican gimnasia.
Para este primer ejemplo prepararemos una tabla en sentido vertical, tal como la que vemos:
|
deporte |
socios |
|
Natación |
200 |
|
Fútbol |
350 |
|
Vóleibol |
150 |
|
Baloncesto |
400 |
|
Atletismo |
300 |
|
Tenis |
100 |
|
Balonmano |
240 |
|
gimnasia |
260 |
Datos en forma de ecuación:
Lo que debemos pagar (importe) por una determinada cantidad de bebidas gaseosas lo obtenemos según la fórmula:
Importe = 0,75 · nº de gaseosas
Construyamos una tabla que nos muestre los valores si se compran desde 1 hasta 12 gaseosas:
|
Nº de gaseosas |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Importe |
0,75 |
1,5 |
2,25 |
3 |
3,75 |
4,5 |
5,25 |
6 |
6,75 |
7,5 |
8,25 |
9 |
En las celdas de la primera fila aparece el número de gaseosas que se comprar (desde 1 hasta 12).
En las celdas de la segunda fila aparecen los valores correspondientes al número de gaseosas, calculados a partir de la ecuación dada en el enunciado.
Otro ejemplo:
Si el precio de un viaje en taxi lo calculamos mediante la ecuación (en $) = 220 • distancia (en km) + 1,5 constuir una tabla para recorridos de 2, 3, 5, 7, 8, 10, 12 y 13 km.
La tabla quedará así:
|
Distancia (km) |
2 |
3 |
5 |
7 |
8 |
10 |
12 |
13 |
|
Precio ($) |
441,5 |
661,5 |
1.101,5 |
1.541,5 |
1.761,5 |
2.201,5 |
2.641,5 |
2.861,5 |
Ver: PSU: Matemática; Pregunta 07_2007
Construcción de gráficos (o gráficas)
Se denomina gráfica o gráfico la representación de datos , generalmente numéricos, mediante líneas, vectores, superficies, colores o símbolos , que muestran visualmente la relación que guardan entre sí. También puede ser un conjunto de puntos , que se plasman en coordenadas cartesianas , y sirven para analizar el comportamiento de un proceso, o un conjunto de elementos o signos que permiten la interpretación de un fenómeno.
Los medios de comunicación nos ofrecen constantemente noticias ilustradas con gráficas.
|
Una gráfica, entonces, permite representar la relación existente entre una lista de elementos (como temperatura, tiempo, espacio, etc.) y sus valores numéricos correspondientes.
Asi, podemos decir que las gráficas tienen como función fundamental representar visualmente, en forma clara e intuitiva, una serie de datos que aportan gran cantidad de información.
Según su construcción, podemos distinguir dos tipos de gráficas: Gráficas cartesianas y Graficas estadísticas
Construcción de gráficas cartesianas
Si lo que queremos es mostrar la relación entre dos variables, podemos hacerlo mediante una gráfica cartesiana.
Las variables que se presentan en el eje horizontal o eje x (abscisas) en una gráfica cartesiana se llaman variable independiente y las que se representan en el eje vertical o eje y (ordenadas) , se llaman variable dependiente .
Aquí debemos anotar que en una gráfica cartesiana no tienen por qué coincidir las unidades de medida de los dos ejes, sino que los datos se acomodan a su propia escala.
|
Los datos para construir una gráfica cartesiana pueden provenir de texto , o pueden obtenerse a partir de tablas o a partir de fórmulas .
a) Construcción de gráficas cartesianas a partir de textos.
Ejemplo:
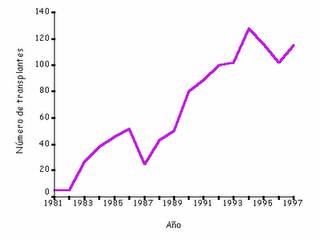
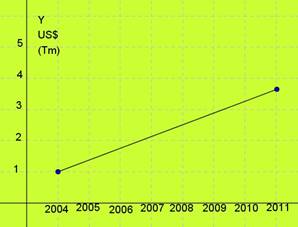
El precio del cobre ha subido en forma sostenida desde 2004, como se aprecia en el gráfico de la izquierda.
Por lo general, en estos casos no importa mucho el valor exacto de los puntos, sino el dibujo, que indica la forma global de la gráfica y el comportamiento de las variables.
b) Construcción de gráficas cartesianas a partir de tablas
A veces resulta muy clarificador que los datos recogidos en una tabla se representen gráficamente sobre unos ejes de coordenadas.
Veamos cómo representar gráficamente los datos de la siguiente tabla de valores:
|
Tabla de valores |
|
|
x |
y |
|
0 |
6 |
|
1 |
1 |
|
2 |
9 |
|
3 |
2 |
|
4 |
3 |
|
5 |
5 |
|
6 |
4 |
|
7 |
7 |
|
8 |
6 |
|
9 |
3 |
|
10 |
8 |
|
11 |
9 |
|
12 |
2 |
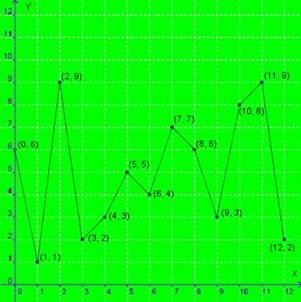
Ahora dibujaremos un sistema de ejes coordenados (figura abajo) sobre el que representaremos los datos, marcando los valores correspondientes tanto en el eje de abscisas (X) como en el eje de ordenadas (Y) :
|
En nuestra gráfica hemos unido, mediante segmentos, cada par de puntos consecutivos, aunque no siempre se deberán unir.
Siempre que se puedan unir los puntos mediante segmentos diremos que la gráfica es continua , y cuando no sea posible hacerlo, diremos que la gráfica es discontinua .
Veamos un ejemplo de gráfica discontinua:
Tenemos una tabla que nos muestra el tiempo (en horas) que emplean 15 atletas en completar un recorrido:
La tabla entrega estos datos:
| Nº atletas |
Tiempo (h) |
|
1 |
8 |
|
3 |
7 |
|
2 |
6 |
|
4 |
5 |
|
5 |
4 |
La gráfica resultante, a partir de esta tabla sería esta :
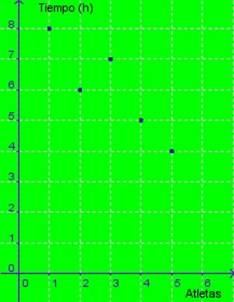
|
Veamos ahora un ejemplo de gráfica continua
Tenemos un tabla que nos muestra los kilómetros recorridos por un ciclista en el transcurso de 5 horas:
| Horas |
Kms recorridos |
|
1 |
20 |
|
2 |
40 |
|
2,5 |
50 |
|
3 |
60 |
|
3,5 |
60 |
|
4 |
60 |
|
5 |
70 |
La gráfica resultante a partir de esta tabla será :
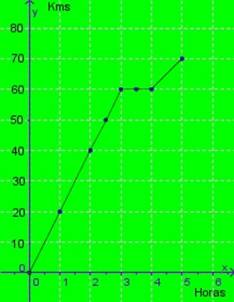
|
Esta es una gráfica continua ya que podemos unir los puntos mediante segmentos debido a que es posible considerar un valor intermedio para el tiempo, ya que a las 2,5 y a las 3,5 horas también podemos anotar los kilómetros recorridos.
c) Construcción de gráficas a partir de fórmulas
En algunos casos la información recopilada o entregda llega por medio de fórmulas o reglas que nos permiten relacionar variables distintas y así elaborar tablas de valores, las cuales podemos transformar en gráficas.
Veamos un ejemplo:
El costo (valor o importe) de un litro de gasolina (nafta o bencina) es 1,2 dólar ( 1,2 US$). Sabido esto, elaborar la gráfica que relacione ese precio unitario con la cantidad de litros que se compren:
Primero, hacemos una tabla para saber el costo de 1, 2, 3, 4, 5 y 6 litros :
|
Litros |
Precio (US$) |
|
1 |
1,2 |
|
2 |
2,4 |
|
3 |
3,6 |
|
4 |
4,8 |
|
5 |
6 |
|
6 |
7,2 |
Trasladamos los datos a una gráfica, que sería (gráfica siguiente) :
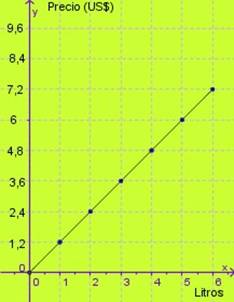
|
Tipos de Gráficas estadísticas
Hasta aquí hemos visto solo gráficas cartesianas , construidas sobre la base de un Plano cartesiano .
Existen otras formas gráficas de representar datos, que son las siguientes:
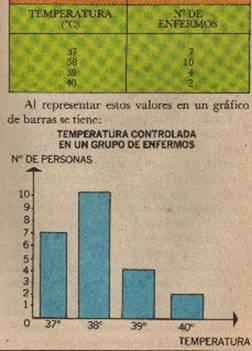
a) Gráfico de barras :
Es un gráfico estadístico que está formado por varios rectángulos igualmente espaciados, del mismo ancho, cuyas bases están colocadas sobre una misma línea horizontal.
|
|
|
Gráfico de barras
|
A los rectángulos que forman el gráfico de barras se les llama barras.
En este tipo de gráfico, es posible observar que las barras:
1.- Están sobre el eje de las abscisas .
2.- Tienen el mismo ancho.
3.- Están igualmente espaciadas.
En el eje de las abscisas se representan los valores de una de las variables (eje x) y en el eje de las ordenadas se representa la otra variable (eje y).
Se usa generalmente cuando se pretende resaltar la representación de porcentajes de datos que componen un total.
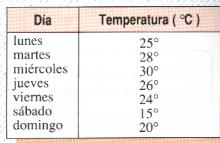
b) Gráfico lineal o de segmentos :
Se usa especialmente para representar datos numéricos de situaciones que ocurren en períodos sucesivos. Además permite visualizar rápidamente una situación determinada.
|
|
Tabla temperatura por día
|
En el ejemplo (tabla arriba) , los datos numéricos corresponden a las temperaturas máximas registradas durante una semana del mes de octubre; estos datos son números que se obtuvieron en forma sucesiva, día tras día.
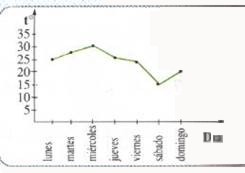
En el gráfico lineal de abajo (construido a partir de la tabla de valores anterior) se puede visualizar fácil y rápidamente que el día miércoles de esa semana se registró la temperatura más alta, y también que el día jueves fue la más baja.
|
|
|
Gráfico lineal |
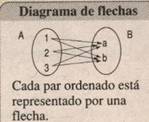
C) diagrama:
|
|
| Gráfico de flechas |
Un elemento de la derecha se relaciona con uno de la izquierda.
d) Gráfico circular:
Muestra las relaciones o proporciones de las partes con un todo. Este gráfico (abajo) es de utilidad cuando se pretende destacar un elemento importante.
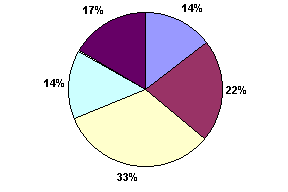
|
Un gráfico circular siempre se compone de una serie de datos.
e) Gráfico de puntos:
El denominado gráfico de puntos permite mostrar apropiadamente a pequeños conjuntos de datos y tiene la gran ventaja de ser fácilmente construido a mano.
En este tipo de gráfico, la abcisa (línea horizontal) representa los valores de la variable estudiada y la ordenada (línea vertical) la frecuencia de aparición de un valor en el conjunto de datos estudiado.
Comentario pedagógico.
Para la construcción de un gráfico de puntos, es necesario que el alumno conozca la representación de puntos en una recta graduada.
Por ejemplo, el siguiente gráfico representa una alumna de cuarto medio cuya altura es 162 cm.
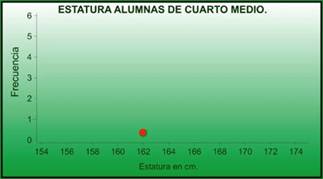
Si hubiese que representar otra alumna con esta misma estatura, el gráfico se vería de la siguiente forma:
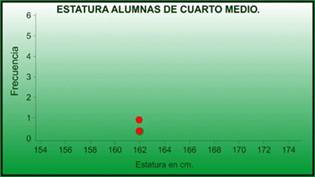
Ahora, si se quisiera representar una muestra de la estatura de treinta alumnas de cuarto año medio, el gráfico quedaría como sigue.
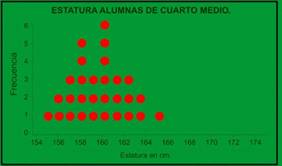
Se puede ver con facilidad la distribución de los valores observados y describir la información contenida en ellos.
Ver: PSU: Matemática, Pregunta 04
Ir a: Más sobre gráficas cartesianas
Fuentes Internet:
http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena11/1quincena11.pdf
http://es.wikipedia.org/wiki/Gr%C3%A1fica
http://jeffgrajales.blogspot.com/
Para practicar
http://www.edu.xunta.es/espazoAbalar/sites/espazoAbalar/files/datos/1285583725/contido/index.html
http://www.amolasmates.es/EDUCAREX/SEGUNDO/graficas/index.html
Ejericicos de interpretación en:
http://www.amolasmates.es/anaya/anaya1ESO/datos/14/05.htm
Tratamiento de la información. Análisis de tablas y gráficos (8º básico)
https://www.codelcoeduca.cl/minisitios/docentes/pdf/matematica/2_matematica_NB6-8B.pdf