Ecuaciones: Ayuda para resolver problemas |
Una de las mayores dificultades que tienen los alumnos es convertir el lenguaje coloquial en símbolos matemáticos y viceversa, lo cual muchas veces les impide resolver algunos problemas que se les plantean.
El problema se agrava cuando se presentan los "problemas de aplicación" , ya que muchos de ellos están fuera de su entorno de conocimientos.

|
| Transformar el lenguaje cotidiano en símbolos matemáticos. |
Por lo general, para aplicar conocimientos de matemáticas y poder proponer modelos de solución, los alumnos requieren de conocimientos básicos de otras áreas; este asunto plantea mayor dificultad que el poder despejar una ecuación.
La mejor recomendación es la práctica cotidiana; en la medida que los alumnos realizan ejercicios, progresarán en la adquisición del conocimiento.
Es importante notar que hay una diferencia básica entre el concepto "problema" y "ejercicio" .
No es lo mismo hacer un ejercicio que resolver un problema. Una cosa es aplicar un algoritmo de forma más o menos mecánica, evitando las dificultades que introduce la aplicación de reglas cada vez más complejas, y otra, resolver un problema, dar una explicación coherente a un conjunto de datos relacionados dentro del contexto.
La respuesta suele ser única, pero la estrategia resolutoria está determinada por factores madurativos o de otro tipo.
Una parte importante de los errores en la resolución de problemas son las dificultades de comprensión lectora . La tendencia de operar todos los datos presentados, aunque algunos no sirvan, certifica esta falta de comprensión global.
Por otra parte, los alumnos resuelven mejor los problemas si alguien se los lee que si los lee él mismo.
Como pauta general para resolver problemas matemáticos, los alumnos deben:
Analizar y comprender el enunciado, para ello deben subrayar las palabras más significativas del mismo, para defiinir aquellas que dan las órdenes.
Luego expresar el problema en lenguaje simbólico o matemátcio. Las ecuaciones sirven a menudo para resolver problemas. Debemos recordar que en una ecuación la variable puede estar representada por cualquier letra, por costumbre, se usa "x" .
Luego se resuelve la ecuación, se verifican sus resultados y se entrega la respuesta.
A continuación, entregamos una tabla de equivalencias entre una expresión coloquial y su simbología, la cual puede resultar muy útil si es consultada a menudo:
| Expresión coloquial |
Simbología matemática |
|
Dado un número |
|
|
El duplo, el doble de un número |
|
|
La mitad de un número |
|
|
Un número disminuido en ... |
|
|
El antecesor , o el anterior de un número |
|
|
El sucesor , el consecuente , o el siguiente de un número |
|
|
El opuesto de un número |
|
|
Números consecutivos |
|
|
Un número par |
|
|
Números pares consecutivos |
|
|
Un número impar |
|
|
Números impares consecutivos |
|
|
El triple de un número |
|
|
El cuádruplo de un número |
|
|
La tercera parte, o el tercio de un número |
|
|
La cuarta parte de un número |
|
|
La quinta parte de un número |
|
|
El cuadrado de un número |
|
|
El cubo de un número |
|
|
El cuadrado del siguiente de un número |
|
|
El cubo del siguiente de un número |
|
|
La raíz cuadrada de un número |
|
|
La raíz cúbica de un número |
|
|
La raíz cuarta de un número |
|
|
La razón entre dos números: división |
|
|
El producto entre dos números: multiplicación |
|
|
La diferencia entre dos números: sustracción |
|
Ver, además: Lenguaje algebraico
A modo de ejemplo:
La suma de tres números naturales consecutivos (lenguaje coloquial) es 45. ¿Cuáles son dichos números?
Procedimiento:
1.- Buscamos en la tabla cómo simbolizar números consecutivos, y nuestro problema indica sumar tres de ellos:
![]() (simbología matemática)
(simbología matemática)
2.- Como la operación es la suma de tres números, no necesitamos usar paréntesis
3.- Planteamos la ecuación:
![]()
4..- Resolvemos la ecuación: sumamos los términos semejantes entre sí:
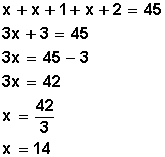
5.- Ahora conocemos el primer número, y para hallar los dos siguientes hacemos:
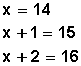
6.- Verificamos y hacemos
![]()
Ver Ejercicios de ecuaciones con formato textual
Ver: Concepto de ecuación
Ver: Ecuaciones de primer grado

