Ecuación cuadrática binomial

Ecuaciones cuadráticas binomiales son aquellas que se presentan de la forma

ax² +  bx  =  0;  donde "a" es distinto de cero  (a   ≠  0)

Este tipo de ecuaciones se puede resolver usando la fórmula general para las cuadráticas, pero para las cuadráticas binomiales hay un camino distinto, que hace mucho más simple la solución.

Para aplicar esta solución debemos recordar que: El producto de dos términos o factores es o será igual a cero, sí, y solo sí, uno de sus factores es cero. 

Esto significa que siempre una de sus raíces o soluciones será cero.

Recordando esto siempre, procedamos:

Primero debes Ver:

Factorizar en:

https://www.profesorenlinea.cl/matematica/AlgebraFactorizacion.htm

Sigamos:

Si tenemos la ecuación cuadrática binomial

ax² +  bx  =  0;  lo primero que debemos hacer es factorizarla

x (ax  +  b)  =  0  (el factor común es la x)

Como dijimos arriba, una de las soluciones será cero; entonces, si x  =  0

ax  +  b  =  0,  resolvemos y queda

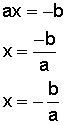
que es la segunda raíz o solución para la ecuación dada.

Entonces las soluciones o raíces de la ecuación dada son:

x  =  0

x = – b/a

Veamos el siguiente ejercicio:

2x² – 3x  = 0

Primero, factorizamos:

x (2x –  3) = 0; si x es =  0, nos queda

2x –  3  =  0, y al resolver tenemos

2x  =  3

x  = 3/2

Las raíces o soluciones de esta ecuación cuadrática binomial son  x  =  0   y   x  = 3/2

Ejercicios de práctica:

a) 12x –  x²  =  0

Factorizamos:

x(12 – x) = 0

si x  = 0; entonces  (es algo así:   0 (12 – x)  = 0, pero ese cero antes del paréntesis no se pone)

Por lo tanto;

12 – x  = 0

– x  =  – 12

x = 12

Soluciones o raíces:  x  =  0;   x   =  12

b)  x² –  9x

Factorizamos:

x (x  - 9)  = 0

si x = 0; entonces

x – 9 = 0

x = 9

Soluciones o raíces:  x  = 0;  x = 9

c)

Factorizamos:

Si x  =  0

Entonces

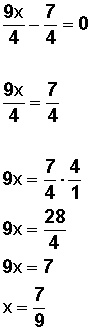
Soluciones o raíces:  x  = 0;  x = 7/9

d) 6x – 0,06x²  = 0

Factorizamos:

x(6 – 0,06x) = 0

Si x  =  0; entonces

6 – 0,06x = 0

– 0,06x = – 6

x = 6/0,06

x = 100

Soluciones o raíces:  x  = 0;  x = 100

e) 0,01 x² – 0,1 x = 0

Factorizamos:

x(0,01x – 0,1) = 0

Si x  = 0; entonces

0,01x – 0,1  = 0

0,01x = 0,1

x = 0,1/0,01

x  = 10

Soluciones o raíces:  x  = 0;  x = 10

Y, por último, resolvamos la siguiente ecuación cuadrática binomial:

(x  +  5)²    =  25

Resolvemos el cuadrado del binomio (x + 5)²

(x +5)(x +5) = x² +10x + 25

Igualamos a cero la ecuación

x² + 10x + 25 = 25

 pasando el 25 de la derecha hacia la izquierda (con signo cambiado)

x² +10x + 25 – 25 = 0

Para quedar

x² +10x  = 0

Factorizamos

x(x + 10 ) = 0

Si x  = 0; entonces

x + 10 = 0

x = –10

Soluciones o raíces:  x  = 0;  x = – 10

Ver: Ecuaciones cuadráticas en:

https://www.profesorenlinea.cl/matematica/Ecuaciones_Seg_grado.html