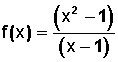Identificar Dominio en una función |
Recordemos:
En una función, el Dominio lo forman las preimágenes o valores de entrada (los valores de x).
La Imagen es el resultado para y [o f(x), que es lo mismo], o valores de salida, según sea el valor de x (las imágenes forman el recorrido).
Para describir matemáticamente el dominio de una función, se usan tanto los corchetes "[,]" como los paréntesis "(,)".
Se usa un corchete cuando el número está incluido en el dominio y se usa un paréntesis cuando el dominio no incluye el número.
La letra U indica una unión que conecta partes de un dominio que podrían estar separadas por un espacio.
Por ejemplo, un dominio de [–2, 10) U (10, 2] incluye –2 y 2 pero no incluye el número 10.
Nota: Siempre usar paréntesis si incluimos el símbolo de infinito (∞).
Entonces, como corolario:
El paréntesis cerrado [ o ] significa que el valor está incluido en el intervalo.
El paréntesis abierto ( o ) significa que el valor no está incluido en el intervalo.
Ahora, vamos al grano.
Las funciones pueden ser de diferente tipo, tenemos:
Funciones lineales
Funciones polinómicas
Funciones cuadráticas
Funciones racionales (con fracciones)
Funciones con radicales (raíces).
En general, en todas las funciones se pueden obtener valores de salida que están dentro de los números reales (R); pero hay que considerar que en algunas funciones es posible que no todos los valores de entrada sean válidos.
Por ejemplo, una función no se cumplirá si se forma con valores equivocados (como una edad negativa).
Tampoco se cumplirá si una función racional (con fracciones) tiene denominador cero.
También ayuda mucho saber el tipo de valores de salida (por ejemplo, que sean siempre positivos).
Por tanto, necesitamos identificar todos los valores (hallar el Dominio) que pueden entrar y salir de una función.
O, dicho de otro modo, tenemos que identificar aquellos valores que no cumplen con la función.
Conocer el Dominio en una función lineal
Veamos cómo hallar el Dominio (Dom o D) en una función lineal de la forma
f(x) = x + 5
En este caso, la x (equis) puede tomar cualquier valor dentro de los Reales ( R )
Dom f(x) = x + 5 R (todos los reales) y su notación será
‒ ∞ < x < ∞
y su intervalo se anota (‒ ∞, ∞)
Conocer el Dominio en una función cuadrática
Tenemos la función cuadrática de la forma
f(x)= x2 + 3 x + 5
tal como en el caso anterior de las lineales, el Dominio son todos los números reales:
Dom f(x) = x2 + 3x + 5 R (todos los reales) y su notación será
‒ ∞ < x < ∞
y su intervalo se anota (‒ ∞, ∞)
Conocer el Dominio en una función racional (con fracciones)
Tenemos la función de la forma
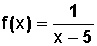
Aquí, el asunto cambia.
Tenemos que analizar lo siguiente: un racional (una fracción) no puede existir si su denominador es igual a cero.
Por lo tanto, si x – 5 fuese igual a cero, no hay función
Entonces, tenemos que buscar un valor de x para que, restado a 5, dé cero:
x – 5 = 0
x = 5
Esto significa que esta función será valida con todos los números reales, menos con el 5, y su notación será
x < 5 o x > 5
y su intervalo se anota (‒ ∞, 5) U (5, ∞).
Esto significa que el Dominio para esta función está entre 5 hacia el menos infinito y entre 5 hacia el más infinito, sin que el 5 participe (lo que se señala con el paréntesis redondo).
Veamos un ejercicio:
Determinar el Dominio para
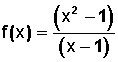
Lo primero es determinar los valores para los cuales no está definida la función. Para ello, igualamos el denominador a cero:
x – 1 = 0
x = 1
Por tanto, el dominio estará formado por todos los reales, excepto para x = 1, lo cual se escribe así:
Dom f(x) = R – {1}
Y su intervalo se anota (– ∞ , 1) U (1 , + ∞ )
Conocer el Dominio en una función con radicales (raíces).
En estos casos, se presenta otro elemento que debe ser analizado.
Hay que fijarse en el índice de la raíz, para saber si es par o impar.
Si el índice es impar (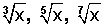
), su Dominio estará en todos los Reales.
Ejemplo:
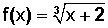
Su Dominio está en todos los Reales: Dom f(x) = R
Ahora, si el índice es par (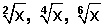
) debemos saber que no existe raíz si el número es negativo.
Ejemplo:
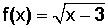
Si x – 3 fuese negativo, no existe esa raíz; por lo tanto, para que x – 3 no sea negativo es obligatorio que x sea igual o mayor que 3.
Si es igual a 3, daría cero y la raíz de cero sería cero, lo cual es válido.
Entonces, para que x – 3 no sea negativo:
x – 3 ≥ 0
x = ≥ 3 (equis debe ser igual o mayor que 3).
El Dominio de esta función está entre 3 (incluido) y más infinito, y lo anotamos
Dom f(x) = [3, + ∞)
Otro ejemplo:
Determinar el Dominio para
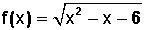
Hacemos
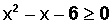
Resolvemos la ecuación de segundo grado, y resulta que
x = 3
x = – 2
Entonces
Dom f(x) = (– ∞, – 2] U [3, + ∞), lo cual significa que el Dominio para esta función está en la unión de dos partes:
entre el menos infinito y el menos 2 incluido, en unión con entre el 3 (incluido) y el más infinito.
Ver: Resolución de ecuaciones de segundo grado.
