Un segmento circular es aquella parte de un círculo que se encuentra delimitada por una cuerda y por el arco que subtiende esta misma cuerda.

En la figura, la parte coloreada corresponde al segmento circular.

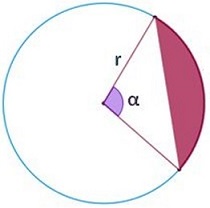
Segmento circular.

Si la cuerda corresponde con el diámetro del círculo, el segmento circular será un semicírculo, y abre un ángulo de 180°.

Ahora bien, todo segmento circular forma parte de un sector circular.

Un sector circular es la parte del círculo comprendida entre dos radios y el arco delimitado por dichos radios.  En la figura, la parte coloreada corresponde al sector circular.

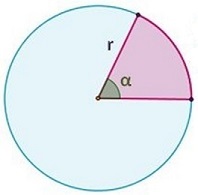
Sector circular.

El área del segmento circular es igual al área del sector circular menos el área del triángulo que forman los puntos del sector circular.

La fórmula para calcular el área del segmento circular, teniendo el ángulo expresado en grados es:

Ahora, si los ángulos se expresan en radianes, la fórmula será:

Nota:

Dependiendo de los datos que se tengan para solucionar un ejercicio, también es posible calcular por separado el área del sector circular y el área del triángulo que se forma bajo el segmento circular.

Más tarde lo veremos con un ejemplo.

Área del sector circular

Calcular o conocer el área de un sector circular,  depende del valor del radio (r) del círculo dado y del ángulo del sector circular (α).

Si dicho ángulo se expresa en grados, la fórmula para calcular el área del sector circular será:

Si el ángulo se expresar en radianes, la fórmula sería:

Ejercicio 1

Hallar el área de un segmento circular cuya cuerda es el lado de un cuadrado inscrito de 10 cm de lado, como se muestra en la figura

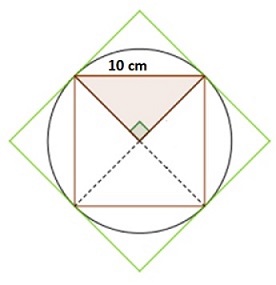
Solución:

Primero, hay que calcular el valor de la diagonal del cuadrado, que será igual al diámetro del círculo.

Esto para obtener luego el valor del radio, que es un lado del triángulo que se forma bajo el segmento circular.

La diagonal forma un triángulo isósceles con dos de los lados del cuadrado (10 cm cada lado), y la diagonal es la hipotenusa de este triángulo; entonces, por el Teorema de Pitágoras:

c²   = a²  +  b²

c² = 10²  +  10²

c²  = 200

c  =  raíz de  200

c   =  14,14 cm   =  diagonal del cuadrado = diámetro del círculo, por tanto:  r  = 7,071 cm (la mitad de la diagonal).

Ahora tenemos los tres lados de un triángulo recto que pertenece al sector circular y que se ubica debajo del segmento circular.

En seguida, calculamos el área del sector circular (usando la fórmula indicada arriba), y le restamos el área del triángulo rectángulo para obtener el área del segmento circular.

Veamos, área del sector circular:

Ahora calculamos el área del triángulo:

Conocemos un lado del cuadrado (10 cm) y este se divide en 4 triángulos iguales; por lo tanto,

Área del cuadrado = 10 * 10 = 100 cm²

Área de cada uno de los 4 triángulos iguales =  25 cm²

Nota.

También podemos calcular el área del triángulo, si multiplicamos base (b) por altura (h) y dividimos entre dos:

b = 7,071

h  = 7,071

7,071  *  7,071  = 49,999, que redondeado da exactamente 50, dividido entre  2  = 25  cm²

Y ahora, al área del sector circular (39,25) le restamos el área del triángulo (25), y queda el área del segmento circular.

Área segCir  =  39,25  -  25   =  14,25  cm²

Respuesta:  14,25 cm², área del segmento circular

Ejercicio 2

Hallar el área del segmento circular coloreado en la figura, donde el radio es 3 cm y el ángulo α es igual a 120°.

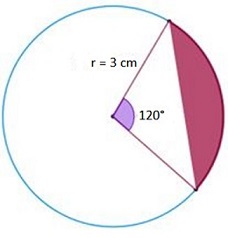
Para hallar el área del segmento circular, podemos aplicar la fórmula:

Tenemos los siguientes datos:

α = 120°

π  = 3,14

senα = 0,866 (obtenido con calculadora)

r = 3

Y reemplazamos en la fórmula:

Ejercicio 3

Hallar el área del sector circular de un círculo de radio 3 cm y que abarca un ángulo de 45° (Π/4 radianes).

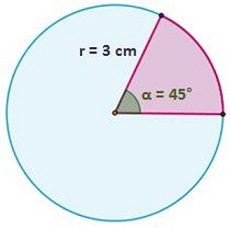
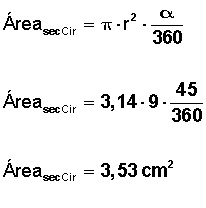
También lo podemos calcular en radianes, obteniendo el mismo resultado:

Descubrimos que su área es de 3,53 cm².