Ángulos y rectas |
Relaciones entre parejas de ángulos
En casi todas las figuras geométricas donde intervengan rectas aparecen ángulos, los cuales es posible relacionar en cuanto a sus dimensiones y a su posición en el plano.
Así, dos ángulos pueden ser entre sí complementarios, suplementarios o adyacentes.
|
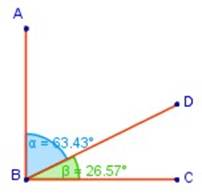
Dos ángulos son complementarios si la suma de sus medidas es 90°
α + β son complementarios α + β= 90°
|
|
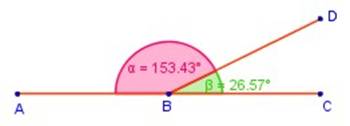
Dos ángulos son suplementarios si la suma de sus medidas es 180°
α + β son suplementarios α + β = 180°
|
|
Dos ángulos son adyacentes si tienen un lado en común y los otros dos están en la misma recta.
Los ángulos adyacentes son suplementarios. |
Rectas secantes y paralelas
Como ya vimos, por definición, un ángulo es una figura geométrica formada en una superficie por dos líneas rectas que parten de un mismo punto.
Fijando nuestra atención en las rectas , sabemos que estas pueden ser secantes (que se cortan) o paralelas (que no se cortan nunca) .
Dos rectas secantes se cortan en un punto y determinan cuatro ángulos. Cada ángulo tiene dos lados y un vértice.
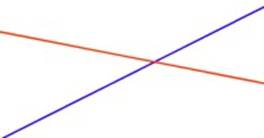
Esta construccción en el plano nos permite relacionar entre sí los ángulos así formados.
Ángulos opuestos por el vértice
|
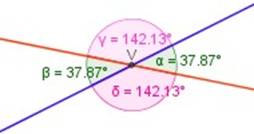
Son los ángulos formados por dos rectas que se cortan en un punto llamado vértice (V) .
α es opuesto por el vértice con β γ es opuesto por el vértice con δ Como podemos verificar en la fígura: Los ángulos opuestos por el vértice son iguales
|
Ángulos determinados por dos rectas paralelas y una secante
|
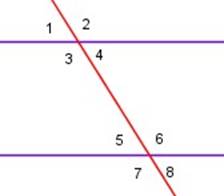
Dos rectas paralelas cortadas por una tercera determinan ocho ángulos:
Esta distribución numérica nos permite carecterizar parejas de ángulos según su posición, haciendo notar que los ángulos 3, 4, 5 y 6 son interiores (o internos) y que los ángulos 1, 2, 7 y 8 son exteriores (o externos) respecto a las rectas:
|
Ángulos internos (3, 4, 5 y 6)
Los ángulos internos a un mismo lado de la transversal a dos rectas paralelas son suplementarios (suman 180º)
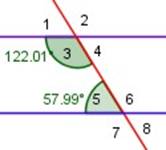
|
|
Ángulos 3 y 5 son suplementarios (suman 180º)
|
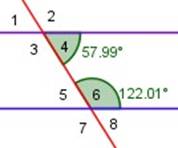
|
|
Ángulos 4 y 6 son suplementarios (suman 180º)
|
Ángulos externos (1, 2, 7 y 8)
Los ángulos externos a un mismo lado de la transversal a dos rectas paralelas son suplementarios .
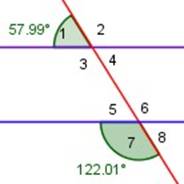
|
|
Ángulos 1 y 7 son suplementarios (suman 180º)
|
|
|
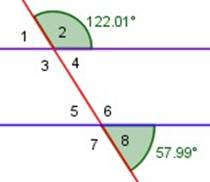
Ángulos 2 y 8 son suplementarios (suman º80º)
|
Ángulos correspondientes :
Son aquellos que están al mismo lado de las paralelas y al mismo lado de la transversal.
|
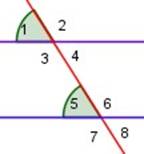
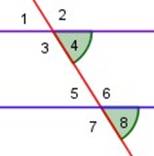
| 1 y 5 son ángulos correspondientes (iguales), ∠ 1 = ∠ 5 |
|
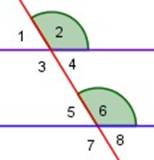
| 2 y 6 son ángulos correspondientes (iguales) ∠ 2 = ∠ 6 |
|
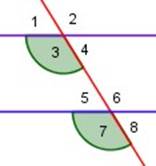
| 3 y 7 son ángulos correspondientes (iguales) ∠ 3 = ∠ 7 |
|
| 4 y 8 son ángulos correspondientes (iguales) ∠ 4 = ∠ 8 |
Esta relación da pie para formular el siguiente postulado:
Si dos rectas paralelas son cortadas por una transversal, entonces cada par de ángulos correspondientes es congruente entre sí.
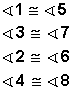
Ángulos alternos internos :
Son aquellos ángulos interiores que están a distinto lado de la transversal y a distinto lado de las paralelas.
|
|
3 y 6 son ángulos alternos internos ∠ 3 = ∠ 6
|
|
|
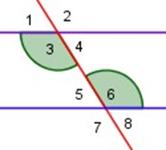
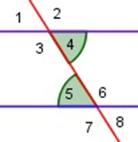
4 y 5 son ángulos alternos internos ∠ 4 = ∠ 5
|
Esta relación da pie para formular el siguiente postulado:
Si dos rectas paralelas son cortadas por una transversal, entonces cada par de ángulos alternos internos es congruente entre sí.
![]()
Ángulos alternos externos:
Son aquellos ángulos exteriores que están a distinto lado de la transversal y a distinto lado de las paralelas.
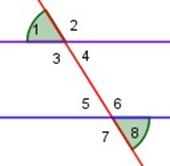
|
|
1 y 8 son ángulos alternos externos ∠ 1 = ∠ 8
|
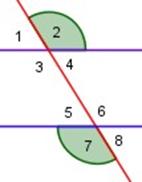
|
|
2 y 7 son ángulos alternos externos ∠ 2 = ∠ 7
|
Esta relación da pie para formular el siguiente postulado:
Si dos rectas paralelas son cortadas por una transversal, entonces cada par de ángulos alternos externos es congruente entre sí.
![]()
Ver: PSU: Geometría; Pregunta 11_2006
Ver: Ángulos en la circunferencia