Ejemplo para dividir un triángulo en 3 partes equivalentes:

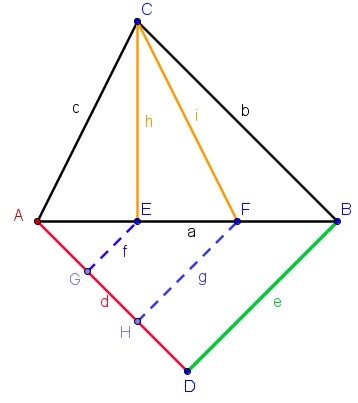
1.- Trazamos una semirrecta en el vértice elegido y la dividimos en 3 partes iguales (o 4, o 5). En la figura de abajo, trazo AD en color rojo.

2.- El último punto obtenido (D) en esta semirrecta lo unimos con el vértice contrario (B) (trazo DB en color verde en la figura) y trazamos paralelas a este trazo, partiendo de los puntos en que hemos dividido la semirrecta inicial. Se obtienen trazos HF y GE (en color azul).

3.- Así tenemos dividido en partes iguales el lado (AB) que enfrenta a la semirrecta trazada.

4.- Cada nuevo punto obtenido (E y F) en dicho lado lo unimos con el vértice opuesto (C) al lado y obtenemos, a partir de ese vértice, tantos triángulos equivalentes como divisiones tengamos.

Veamos otro caso:

Dividir un triángulo dado en varias partes equivalentes (misma área) a partir de un lado.

Ejemplo:

Dividir el triángulo ABC en 5 partes equivalentes partiendo del lado B y llegando al lado C.

1.- Con el compás, trazamos el semicírculo entre A y C (centro en A y diámetro AC)

2.- Operamos como en el caso anterior para dividir el lado deseado en tantas partes iguales como queramos (obtenemos puntos 1, 2, 3 y 4 en el trazo AC).

Como indica la siguiente figura:

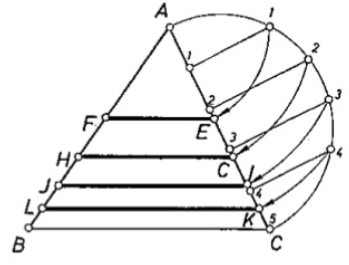
3.- Desde cada uno de estos puntos (1, 2, 3 y 4 en el trazo AC) elevamos una perpendicular hasta cortar el semicírculo anterior (ahora obtenemos puntos 1, 2, 3 y 4 en dicho semicírculo).

4.- Con el compás, hacemos centro en A y con radio A-1 (el 1 del semicírculo) describimos un arco hasta tocar el trazo AC, y obtenemos el punto E.

Con el compás, hacemos centro en A y con radio A- 2 (el 2 del semicírculo) describimos un arco hasta tocar el trazo AC, y obtenemos el punto C.

Con el compás, hacemos centro en A y con radio A-3 (el 3 del semicírculo) describimos un arco hasta tocar el trazo AC, y obtenemos el punto I.

Con el compás, hacemos centro en A y con radio A- 4 (el 4 del semicírculo) describimos un arco hasta tocar el trazo AC, y obtenemos el punto K.

5.- Partiendo desde estos nuevos puntos en el trazo AC, hacemos paralelas a BC (resultan los trazos EF, CH, IJ, KL, todos paralelos a BC) que nos entregan el triángulo dividido en 5 partes equivalentes en área.