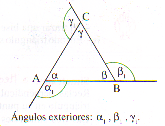Elementos del triángulo |
|
El triángulo es el polígono más simple y también el más fundamental, ya que cualquier polígono puede resolverse en triángulos; por ejemplo, trazando todas las diagonales a partir de un vértice, o, más en general, uniendo todos los vértices con un mismo punto interior al polígono.
Un triángulo tiene elementos primarios y elementos secundarios . Los elementos primarios corresponden a los vértices, lados, ángulos interiores y ángulos exteriores. Los elementos secundarios corresponden a la altura, bisectriz, simetral, transversal de gravedad y mediana. |
Elementos primarios de un triángulo
|
Vértices Son los puntos de origen de los segmentos.
Se nombran con letras mayúsculas: A, B, C ... Z. |
|
Lados
o por una letra minúscula (a, b, c) que corresponde a la letra que nombra el vértice opuesto (A, B, C) .
|
|
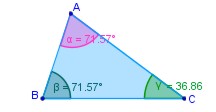
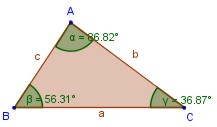
Ángulos interiores Son aquellos formados por cada par de lados consecutivos del triángulo. Se denominan por las tres letras mayúsculas de los vértices o por una letra griega ubicada entre los lados del ángulo.
|
|
Ángulos exteriores Son los ángulos formados por un lado del triángulo y la prolongación de otro hacia la región exterior.
Se nombran generalmente por la letra del ángulo interior adyacente con un subíndice. |
Elementos secundarios de un triángulo
Las líneas notables del triángulo o sus elementos secundarios son:
|
alturas (h)
|
bisectrices (b)
|
simetrales (s)
|
|
transversales de gravedad (t)
|
medianas
|
|
|
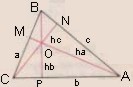
Alturas Son segmentos perpendiculares (segmentos que forman ángulos de 90º) a un lado o a su prolongación desde el vértice opuesto. La altura se designa con la letra h y un subíndice que señala el lado del cual se levanta. Un triángulo tiene tres alturas , una por cada lado (h a , h b, h c ). El punto O donde concurren las tres alturas se llama Ortocentro (O).
El lado y su altura forman un ángulo de 90º. |
|
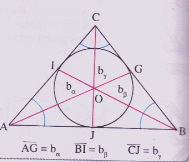
Bisectrices Es la recta que dimidia un ángulo; es decir, es la recta que divide un ángulo en su mitad. Un triángulo tiene 3 bisectrices, uno por cada ángulo y se designan normalmente por la letra b y un subíndice que señala el respectivo ángulo interior.
El punto O donde concurren las tres bisectrices se llama incentro. El incentro corresponde al centro de una circunferencia inscrita en el triángulo. |
|
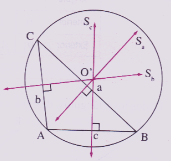
Simetrales o Mediatrices Corresponden a rectas perpendiculares a cada uno de los lados del triángulo en su punto medio. Las tres simetrales se cortan en un punto llamado ( O) circuncentro . La circunferencia pasa por los tres vértices.
Siempre debe tenerse en cuenta que:
|
|
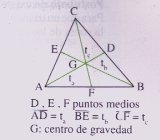
Transversales de gravedad Es el segmento trazado desde un vértice hasta el punto medio del lado opuesto. Todo triángulo tiene tres transversales de gravedad, una por cada lado y se designan normalmente con la letra t y un subíndice que señala el lado (t a, t b, t c ).
El punto donde se intersectan las tres simetrales se llama baricentro y se representa con la letra G. |
|
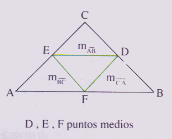
Medianas Son los segmentos que unen directamente los puntos medios de dos lados del triángulo, de dos en dos. La mediana se designa con la letra m y un subíndice que indica el lado sobre el cual se proyecta. La mediana tiene una longitud igual a la mitad del lado paralelo. FD = ½ AC; DE = ½ AB; EF = ½ CB
Al trazar las tres medianas de un triángulo, éste queda dividido en cuatro triángulos congruentes. |
Ver: PSU: Geometría; Pregunta 10_2006