Lo primero es repasar y entender el concepto de ecuación de la recta, en:

https://www.profesorenlinea.cl/geometria/Recta_Ecuacion_de.html

Ejercicio 1)

Determinar si este par de ecuaciones representan rectas paralelas 

x ‒ 3y = 0

3x + y = 0

Ahora, para determinar si un par de rectas son paralelas o perpendiculares entre sí, debemos conocer sus pendientes (m), la que está dada en la ecuación explícita de una recta, que es:

y = mx + b

Entonces, las ecuaciones de rectas dadas debemos llevarlas a la forma explícita, que es lo mismo que resolver para y (ye).

La primera:

x ‒ 3y = 0

resolvemos para y (ye) y queda

‒ 3y = x

el ‒ 3 pasa a la derecha como divisor

y = ‒ x/‒ 3

lo que corresponde a 1/3 x.

Ojo que en estas ecuaciones b = 0.

y = ‒1/‒3 x 

resulta que m = 1/3

La segunda ecuación de la recta:

3x + y = 0

y = ‒ 3x

resulta que m = ‒ 3

He aquí lo importante:

Para que un par de rectas sean paralelas, sus pendientes (m) deben ser iguales.

Las ecuaciones dadas señalan que la pendiente m vale 1/3 en una y que la pendeinte m vale ‒ 3 en la otra; por lo tanto, no son paralelas.

Otra información importante nos dice que un par de rectas son perpendiculares entre sí cuando la multiplicación de sus pendientes es igual a menos 1; veamos:

Por lo tanto, son rectas perpendiculares entre sí.

Ejercicio 2)

Mediante un método gráfico determine si las rectas L1y L2 son paralelas 

L1: y = 2x 1.      L2: y = 4 + 2x

Veamos si sus pendientes (m) son iguales:

Recordemos la forma explícita de la ecuación de la recta:

y = mx + b

Recuerden que b representa el punto donde la recta intercepta la vertical y.

Entonces

y  = 2x ‒ 1

y  = 2x + 4

en ambas ecuaciones la pendiente m vale 2; por lo tanto, son ecuaciones que corresponden a rectas paralelas.

Y los datos nos indican que el intercepto en y de la primera está en  ‒1, y el de la segunda está en 4.

Ahora, ¿cómo podemos graficarlas?

Aquí debemos saber que el valor de la pendiente de una recta está dado por cambio en y (∆y) sobre cambio en x (∆x).

Esta es su fórmula:

si m = 2, es lo mismo que 2/1, donde 1 es el cambio en x y 2 es el cambio en y.

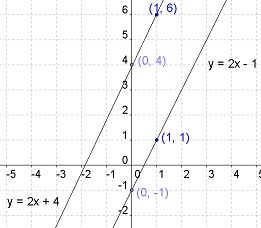
Luego, desde cada punto intercepto movemos un (1) lugar hacia la derecha (cambio en x) y dos (2) lugares hacia arriba (cambio en y).

Los puntos resultantes los unimos con su respectivo intercepto y vemos que obtenemos dos rectas paralelas.

Ejercicio 3)

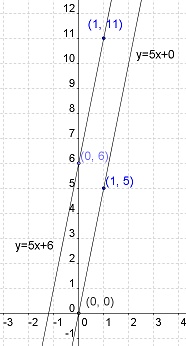
La ecuación de una recta  está dada por y = 5x + 6, determina la ecuación de una recta paralela t, y que pase por  el  punto 

a) (‒ 2, 3)      b) (‒ 6, ‒ 9)     c) (0, 0)

Para que una recta sea paralela a otra, sus pendientes deben ser iguales, entonces una recta t paralela será

 y = 5x + b

pero además debe pasar por el punto a) (‒ 2, 3), y con este dato podemos calcular el valor de b (el intercepto).

El par ordenado (‒ 2, 3), nos señala que (x = ‒2) e (y = 3)

Reemplacemos los valores de x e y en la ecuación explícita y = 5x + b:

3 = 5(‒ 2) + b

3 = ‒10 + b

‒ 10 + b = 3

b = 3 + 10

b = 13

la ecuación de la recta paralela t, que pasa por el punto (‒ 2, 3)  será  y = 5x + 13.

Y si pasa por el punto b) (‒ 6, ‒ 9), será:

 y = 5 x + b

‒ 9 = 5 (‒ 6) + b

‒ 9 = ‒ 30 + b

‒ 30 + b = ‒ 9

b = ‒ 9 + 30

b = 21.

Entonces la ecuación de la recta paralela t será y = 5x + 21

Para ejercitar, resuelve si pasa por el punto c) (0, 0).

Su gráfica sería