En este caso, cuando conocemos o nos dan 3 puntos de una circunferencia, para obtener la ecuación de la misma podemos utilizar un sistema de ecuaciones, que pasaremos a explicar:

Primero: Sabemos que la ecuación general que describe o identifica una circunferencia es

x² + y² + Ax + By  + C = 0

fórmula que tiene 3 parámetros por determinar, que son A, B  y C.

Sabemos (o deberíamos saber), que si se tiene un sistema de 3 ecuaciones se pueden determinar los 3 parámetros.

¿Como obtenemos esas 3 ecuaciones?

Simple. Cada uno de los puntos dados o conocidos de la circunferencia (que representan x  e  y) los sustituimos en la ecuación general y de eso resultarán tres ecuaciones con incógnitas A, B  y C.

Veamos un Ejemplo clarificador:

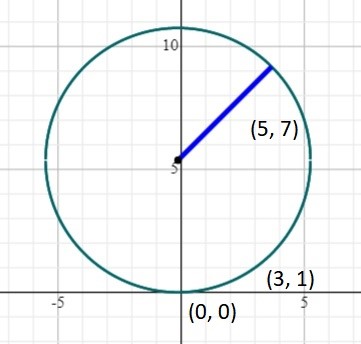
Supongamos que tenemos que describir la ecuación de una circunferencia que pasa por los puntos (0, 0),  (3, 1), y (5, 7) .

Para cada punto sustituimos  x  e  y en la ecuación general de la circunferencia:

Recuerda que en cada par ordenado, como estos que señalan puntos en un plano, el primer dígito representa a la x y el segundo representa a la y)

Entonces

(0, 0)  --> 0²  +  0²  +  A • 0  +  B • 0   +  C = 0  +  0  + 0 +  0 + C  -->  C  = 0

(3, 1)  --> 3²  +  1² + A • 3  +  B • 1  +  C  =  9  +  1  +  A • 3  +  B • 1  + C  =  0

(5,  7) --> 5²  +  7²  +  A • 5  +   B • 7 +  C  =  25  + 49  + A • 5  + B • 7 + C = 0

Ahora, debemos resolver el siguiente sistema de ecuaciones para las incógnitas A,  B  y C:

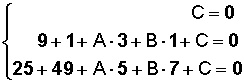
En seguida, sustituimos C (que sabemos vale 0) en las dos ecuaciones siguientes y realizamos las operaciones entre los términos independientes:

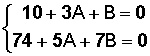
Ahora, podemos aislar B de la primera ecuación:

Y reemplazamos ese valor de B en la segunda ecuación, donde podemos aislar y calcualr el valor de A:

Ahora que conocemos el valor de A (1/4) lo sustituimos en la expresión B =  –10  – 3A:
Para lograr:

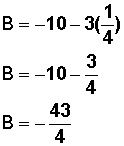
Ahora que conocemos los 3 parámetros (A = 1/4,  B = - 43/4 y C = 0) que determinan la circunferencia, podemos escribir la ecuación que la define:

Y cuya gráfica será