Ejercicio de dilatación y translación

Encuentre el factor de dilatación para la figura

O (2, 5); P (6, 1); Q (0, –1); R (–1, 0),

y su magnitud (valor) de traslación, para que dicha figura dilatada sea trasladada hasta 

A (8, 14); B(16, 6); C(4, 2); D(2, 4).

Solución

Veamos una explicación gráfica de lo que se pide:

Lo primero que debemos hacer es localizar la figura original en el plano cartesiano:

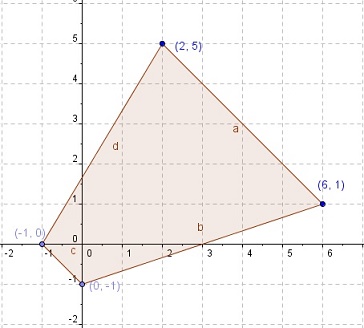
Ahora, como no sabemos el factor de dilatación, localizaremos en el plano la ubicación final de la figura dilatada:

Como paso previo, debemos saber que para dilatar (agrandar proporcionalmente) una figura en el plano hay que multiplicar cada miembro del par ordenado por un factor dado, lo cual nos irá entregando un nuevo par ordenado que señalará el nuevo punto de la figura ahora dilatada.

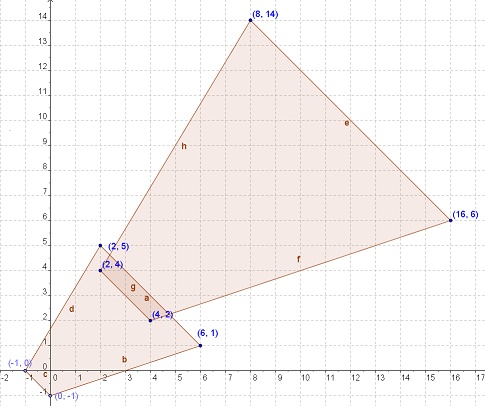
Para encontrar el factor de dilatación y también la cantidad de espacios que movemos para la traslación, hacemos el siguiente razonamiento:

Tenemos el punto O (2, 5), que sabemos se convierte en A (8, 14).

Esto significa que el 2 hay que multiplicarlo por X, luego sumarle Y para obtener 8; igual,  el 5, hay que multiplicarlo por 2, luego sumarle y para obtener 14.

Con estos datos, configuramos el siguiente sistema de ecuaciones:

2x + y = 8
5x + y = 14

Desarrollamos el sistema y obtenemos que x  = 2   e    y  = 4

Ver:

Sistemas de ecuaciones

Seguimos, el factor de dilatación, entonces, es 2 y tendremos la figura original dilatada en:

(2, 5) x 2  = (4, 10)

(6, 1)  x 2 = (12, 2)

(0, - 1) x 2 = (0, - 2)

(- 1, 0 ) x 2 = (- 2, 0)

Que, con fondo violeta, ubicamos en el plano:

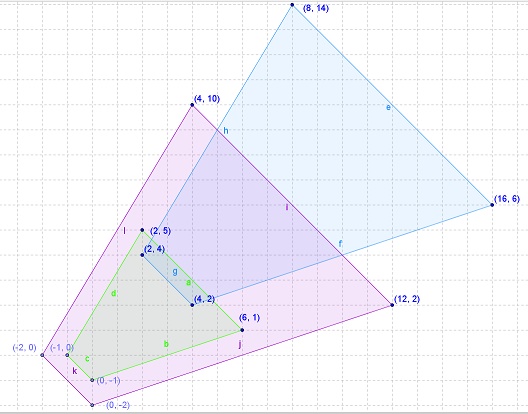
Nota:

Hay que destacar que, al conocer el par ordenado de inicio y el par ordenado final luego de una dilatación y una translación, el sistema de ecuaciones puede establecerse sin necesidad de la explicación gráfica precedente.  Esta se entrega para mayor comprensión del ejercicio y del tema.

Resultado final:

O (2, 5) x 2  = (4, 10) y  para trasladar este nuevo punto dilatado, se suman 4 hacia la derecha y 4 hacia arriba. Y queda A (8, 14)

P (6, 1) x 2  = (12, 2)  y para trasladar este nuevo punto dilatado, se suman 4 hacia la derecha y 4 hacia arriba. Y queda B (16, 6)

Q (0, -1) x 2 = (0, -2) y para trasladar este nuevo punto dilatado, se suman 4 hacia la derecha y 4 hacia arriba. Y queda C (4, 2)

R  ( - 1, 0) x 2 = ( - 2, 0) y para trasladar este nuevo punto dilatado, se suman 4 hacia la derecha y 4 hacia arriba. Y queda D (2, 4)

Para comprobarlo, debes observar el dibujo superior, donde verás 3 figuras semejantes:

la original con puntos (2, 5)  (6, 1)  (0, -1) y (- 1, 0)

la dilatada con factor 2, con puntos (4, 10) (12, 2) ( 0,  -2) y  (- 2, 0)

y la trasladada 4 espacios con puntos (8, 14) (16, 6)  (4, 2) y (2, 4)

Ir a:
Isometría y transformaciones isométricas, en
https://www.profesorenlinea.cl/geometria/Isometria_Transformaciones.html