Imaginemos un plano de dos dimensiones (bidimensional), formado por dos ejes que se cortan perpendicularmente (coordenadas rectangulares como las del Plano Cartesiano).

Llamamos eje y (ye) al vertical y llamamos eje x al horizontal (tal como en el Plano Cartesiano).

En el plano Cartesiano, cada punto está definido por un par ordenado, por ejemplo (4, 5), que nos indica que dicho punto se ubica 4 espacios hacia la derecha en el eje x, y 5 espacios hacia arriba en el eje y, como vemos en la siguiente figura:

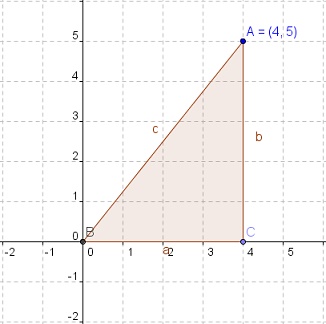
Ese punto A también podemos definirlo usando coordenadas polares, y el par ordenado sería ahora (6, 51°), lo cual nos indica que desde el punto cero (B) hasta el punto A tenemos una medida métrica de 6  (cm o  mm, u otra) y que el  ángulo formado en ABC mide 51°, como vemos en la figura:

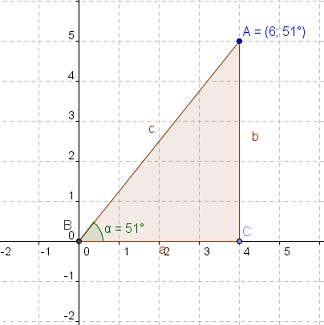
Notas:

1) El valor 6 anotado en la figura es en realidad 6,4 valor que usaremos en los calculos posteriores.

2) En ambas figuras hemos completa el triángulo, uniendo A con C, para una posterior comprensión del tema, cuando usemos trigonometría.

Radio vector y ángulo polar.

El valor de α aumenta si el punto A (en realidad el vector AB, pues la medida se conserva) lo desplazamos en sentido antihorario y disminuye si lo hacemos en sentido horario. La distancia BA ( ≥ 0) se conoce como la "coordenada radial" o "radio vector" (normalmente se identifica como r), mientras que el ángulo formado es la "coordenada angular" o "ángulo polar".

Ahora, podemos decir que las coordenadas polares o sistemas polares son un sistema de coordenadas bidimensional donde cada punto del plano está determinado por una distancia y un ángulo, como se ilustra en siguiente figura:

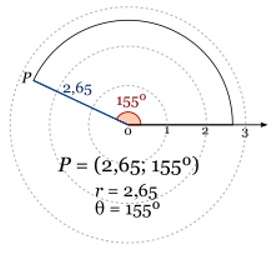
Localización de un punto en coordenadas polares.

En la figura, el punto P está a 2,65 cm (medida de longitud) desde el punto 0 y se abre en ángulo de 155° respecto al eje horizontal y su par ordenado se anotará así: (2,65;  155°).

Convertir coordenadas polares a rectangulares o cartesianas y viceversa

Volviendo a las figuras de arriba, hemos anotado en la primera los valores para el par ordenado (4,  5) que indica la ubicación del punto A en un plano rectangular (como el Plano Cartesiano). Y en la segunda, anotamos los valores para el par ordenado (6,  51°) (en realidad 6,4; 51°) que indica la ubicación del mismo punto A, pero en un plano polar.

Lo anterior significa que cualquier punto en un plano puede expresarse tanto en coordenadas rectangulares (Plano Cartesiano) como en un plano polar (coordenadas polares), pues son equivalentes y se pueden convertir uno en el otro y viceversa.

Convertir de polar a cartesiana

Para esta conversión es que necesitamos conocimientos de trigonometría, en las funciones seno, coseno y tangente  inversa (o arco co-tangente).

Si tenemos las coordenadas polares (un radio y un ángulo), podemos obtener fácilmente la ubicación de x y la ubicación de y en el plano cartesiano, usando las siguientes fórmulas:

Para conocer el valor de x:

x = r cos α   (se multiplica el valor del segmento por el coseno del ángulo)

Veamos si es cierto con los datos de arriba:

x = 6,4 cos α   (cos de 51°  = 0,63)

x =  6,4 (0,63)

x  = 4,3  (redondeamos a 4)

x  =  4

Para conocer el valor de y:

y = r sen α  (se multiplica el valor del segmento ( r ) por el seno del ángulo)

y = 6,4 (sen 51°)  (sen de 51° = 0,78)

y  =  6,4  (0,78) 

y =  4,92   (redondeamos a 5)

Convertir de cartesiano a polar

Usando el mismo ejemplo de nuestros gráficos iniciales transformaremos las coordenadas cartesianas (4, 5) a coordenadas polares:

Recuerden que el 4 es la x y el 5 es la y.

Primero debemos calcular el valor del radio  (el valor del segmento en longitud) para ello usamos la fórmula:

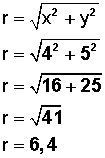
Y tenemos el valor del segmento (r).

Ahora debemos calcular el valor del ángulo:

Para ello, usamos la fórmula

    tangente inversa o arco-cotangente  por y/x

Usamos una calculadora científica y el resultado es 51.

Entonces el ángulo α = 51°

Para una explicación visual

Ver

https://www.youtube.com/watch?v=cSZZW6gDS0w