Círculo de Apolonio o Circunferencia de Apolonio |
Se trata de un famoso problema de lugares geométricos :
Se llama lugar geométrico a un conjunto de puntos que satisfacen determinadas propiedades geométricas.
Respecto al Circulo de Apolonio , dados dos puntos, A y B , se trata de determinar el lugar geométrico de los puntos del plano, P , que cumplen:
![]() , siendo
k
una
constante
.
, siendo
k
una
constante
.
Apolonio
estableció que:
El lugar geométrico de los puntos (P, P 1 , P 2 , P 3 ...) cuya distancia desde un punto fijo (A) es un múltiplo de su distancia desde otro punto fijo (B) es una circunferencia.
Por ejemplo, si dados los puntos A y B , queremos hallar los puntos (P) que distan de A el doble que de B , podemos hacer la construcción siguiente:
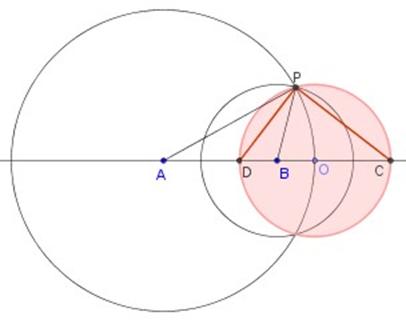
Obtenemos P , uno de los puntos buscados, como intersección de circunferencias con centros A y B , siendo el radio de la primera el doble que el de la segunda ( PA = 2PB ).
Ahora hallamos la bisectriz del ángulo APB la cual corta a la recta AB en el punto D , que es uno de los extremos del diámetro de la circunferencia buscada.
El otro extremo del diámetro ( punto C ) lo obtenemos haciendo el segmento PC , perpendicular a PD (corresponde a la bisectriz de uno de los ángulos exteriores del polígono APD ).
Recordemos que bisectriz exterior es la bisectriz del ángulo exterior de un polígono .
En la siguiente figura se comprueba que:
![]() (constante)
(constante)
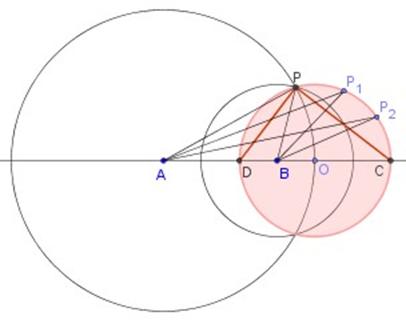
En seguida, podremos ver la circunferencia de Apolonio que se obtiene al considerar los puntos que distan de A el doble que de B . Las circunferencias concéntricas (con centros en A y en B ) nos permiten encontrar puntos de la circunferencia de Apolonio :

Así, el punto C dista 4 unidades desde A y 2 desde B ; el punto D dista 6 unidades desde A y 3 desde B ; el punto E dista 8 unidades desde A y 4 desde B ; el punto F dista 10 unidades desde A y 5 desde B ; el punto G dista 12 unidades desde A y 6 desde B , etc. Estos puntos determinan la circunferencia buscada.
Versiones para el Círculo de Apolonio
Existen dos versiones del círculo de Apolonio , la primera, relacionada con el lugar geométrico de los puntos P, a partir de A y B, que acabamos de ver.
La segunda versión se relaciona con los triángulos , así “si por el vértice de un triángulo se hacen las bisectrices exteriores e interiores de ese ángulo, ambas cortan al lado opuesto al vértice o a su prolongación en dos puntos, la circunferencia de diámetro el segmento entre esos dos puntos da la llamada circunferencia de Apolonio, la cual pasará además por el vértice al que se le hicieron las bisectrices”.
Otra forma de expresarlo, más relacionada con la primera expresión es, “Dado un lado de un triángulo y la razón de longitudes de los otros dos lados, el lugar geométrico del tercer vértice es el círculo de Apolonio, cuyo centro esta en la extensión del lado dado.”
Para un cierto triángulo, hay tres circunferencias de Apolonio.
En la figura siguiente se muestran las tres circunferencias de Apolonio del triángulo ABC . Puede observarse en la figura que, por ejemplo, el centro U de uno de los círculos es la intersección de la recta tangente en el punto A a la circunferencia circunscrita con la prolongación del lado opuesto BC . De forma análoga pueden obtenerse los centros V y W de las otras circunferencias.
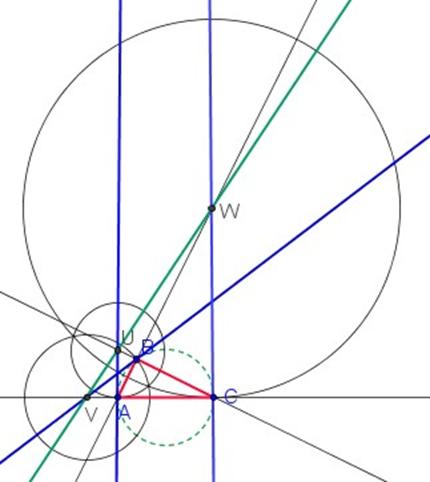
En azul las tangentes a los puntos A, B y C de la circunferencia circunscrita al triángulo.
En verde continuo, la recta de Lemoine.
Recta de Lemoine
En la figura anterior puede apreciarse que los centros de las circunferencias Apolonio de un triángulo están alineados. La recta que los contiene se llama recta de Lemoine (Emile Michel Hyacinthe Lemoine 1840-1912).
Fuentes Internet:
“Apolonio de Perga" Enciclopedia Microsoft® Encarta® en línea 2001
http://encarta.msn.es © 1997-2000 Microsoft Corporation. Reservados todos los derechos.
http://trazoide.com/wiki/index.php?title=C%C3%ADrculo_de_Apolonio
http://www.acm.org.ve/guia-4.pdf
http://menorca.infotelecom.es/~ecampins/Matematiques/2Eso/Apolonio%20de%20Perga.htm
http://garciacapitan.auna.com/bella/htm/circapol.htm
http://www.mat.usach.cl/histmat/html/apol.html
Además, en la página de Internet
http://centros5.pntic.mec.es/~marque12/matem/apolonio.htm
se puede ver una animación (applet) que permite observar la circunferencia de Apolonio correspondiente a los puntos A y B y un valor de r comprendido entre 1,5 y 4,5. En la parte inferior del applet se puede modificar la posición del punto B y del valor de la razón.

