Elementos de la circunferencia y del círculo |
Circunferencia es el conjunto de todos los puntos del plano que equidistan de un mismo punto llamado centro de la circunferencia. El punto centro no pertenece a la circunferencia. La circunferencia se nombra con la letra del centro y un radio.

|
Círculo es la figura plana formada por una circunferencia más toda su región o área interior
Ejemplos prácticos de una circunferencia : Aro, anillo, hula-hula, borde de vaso, la orilla de un plato, etc.
Perímetro de la circunferencia: 2 p · r p · d
Elementos de la circunferencia
Rectas en la circunferencia
|
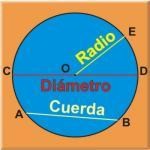
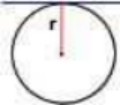
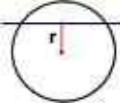
Radio: Es un segmento que une el centro de la circunferencia con cualquier punto de ella. El radio se nombra con la letra “r” o bien con sus puntos extremos. La medida del radio es constante.
|
|
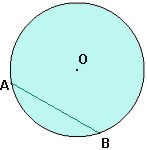
Cuerda: es el segmento que une dos puntos de la circunferencia. Las cuerdas tienen distintas medidas.
|
|
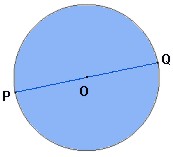
Diámetro: Es la cuerda que pasa por el centro de la circunferencia. El diámetro es la cuerda de mayor medida. El diámetro se nombra con la letra “d”. El diámetro siempre es el doble del radio: d = 2r r = d/2 .
|
|
Tangente: es la recta que intersecta en un solo punto a la circunferencia.
|
|
Secante: es la recta que intersecta en dos puntos a la circunferencia.
|
|
Arco: es una parte de la circunferencia comprendida entre dos puntos de ella.
|
Ángulos en una circunferencia
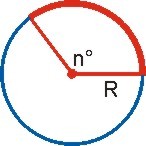
Ángulo del centro: Es el ángulo cuyo vértice es el centro de la circunferencia y sus lados son dos radios de ella.
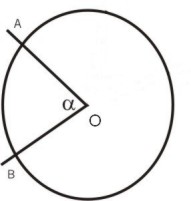
Vértice en el centro de la circunferencia
Lados que contienen radios de ella
m (< AOB) = m (arco AB)
Ejemplo:
|
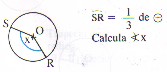
(Debe leerse: arco SR es igual a un tercio de la circunferencia. Calcular el ángulo X)) |
Por definición del Teorema del ángulo del centro la medida del arco SR es igual a la medida del ángulo del centro (x). Como la circunferencia en el sistema sexagesimal tiene 360º significa que el arco SR mide 1/3 de 360º, esto es dividir 360 en 3 partes y tomar 1 sola.
360º : 3 = 120º < SOR = 120º
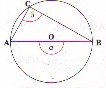
Ángulo Inscrito: Es el ángulo cuyo vértice está sobre la circunferencia y sus lados son cuerdas de ella. Para todo ángulo inscrito, existe un ángulo del centro que subtiende el mismo arco. El ángulo inscrito es igual a la mitad del ángulo del centro que subtiende el mismo arco.
|
Figura
|
|
< ABC inscrito que subtiende arco AC < AOC del centro que subtiende arco AC Vértice en la circunferencia. Los lados son cuerdas de ella. < ABC subtiende arco AC. El centro de la circunferencia está en el interior del ángulo. m ( <ABC) = ½ m (<AOC) (Debe leerse: medida del ángulo (ABC) es igual a la mitad del ángulo (AOC) |
Ejemplo:
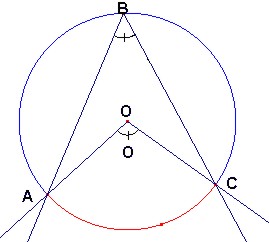
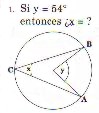
|
Si ángulo y es igual a 54 grados
Entonces ¿cuánto mide el ángulo x ? El ángulo “y” es un ángulo del centro; el ángulo “x” es un ángulo inscrito que subtiende un arco común con el ángulo del centro (AB), por lo tanto, se debe aplicar el Teorema del ángulo inscrito.
Por Teorema:
x = 1/2 y
|
Caso Especial :
|
Si un ángulo inscrito subtiende una semicircunferencia , entonces es recto.
α = 180º β = 90º |
CIRCULO O REGION CIRCULAR: Es todo el espacio interior encerrado por una circunferencia..
REPRESENTACIONES MATERIALES DEL CIRCULO: Disco, plato, fondo de vaso, tapa de tarro, CD, etc
AREA DEL CIRCULO: p · r 2
Elementos del círculo
|
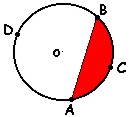
Segmento circular: es cada una de las partes en que se divide un círculo cuando se traza una cuerda (A - B). Si la cuerda es un diámetro, cada parte será un semicírculo.
|
|
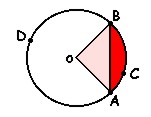
Sector circular: es la parte del círculo limitada por dos radios y un arco .
|
|
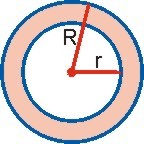
Corona circular: es la porción del plano comprendida entre dos circunferencias concéntricas.
|