Interacción entre cargas eléctricas (Ejercicios) |
Sabemos que la ley de Coulomb es válida sólo en condiciones estacionarias; es decir, cuando no hay movimiento de las cargas, o como aproximación cuando el movimiento es a bajas velocidades y rectilíneo uniforme. Es por ello que es llamada fuerza electrostática .
Para entrar en materia y desarrollar algunos ejercicios sobre interacciones de cargas eléctricas repasemos la Ley de Coulomb , que dice:
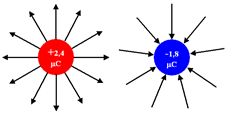
"La fuerza electrostática entre dos cargas puntuales (q 1 y q 2 ) es proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia que las separa, y tiene la dirección de la línea que las une. La fuerza es de repulsión si las cargas son de igual signo, y de atracción si son de signo contrario".
|
| Cargas eléctricas positivas y negativas. |
Vamos por partes:
“La fuerza electrostática entre dos cargas puntuales (q 1 y q 2 ) es proporcional al producto de las cargas”, esto significa que la fuerza de interacción entre dos cargas q 1 y q 2 duplica su magnitud si alguna de las cargas dobla su valor, la triplica si alguna de las cargas triplica su valor y así, sucesivamente.
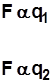
|
(léase F es proporcional a q
1
)
(léase F es proporcional a q 2 )
|
En consecuencia:
|
(léase F es proporcional al producto de q 1 por q 2 )
|
Sigamos:
"La fuerza electrostática entre dos cargas puntuales (q 1 y q 2 ) es inversamente proporcional al cuadrado de la distancia que las separa”, esto significa que si la distancia entre las cargas es r , al duplicarla, la fuerza de interacción disminuye en un factor de 4 (2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar r , la fuerza entre cargas disminuye en un factor de 16 (4²).
En consecuencia:
|
(léase F, la fuerza de interacción entre dos cargas puntuales, es inversamente proporcional al cuadrado de la distancia. |
Asociando ambas relaciones, tenemos:
|
|
Finalmente, se introduce una constante de proporcionalidad (k) para que, en términos matemáticos, la magnitud F de la fuerza que cada una de las dos cargas puntuales q 1 y q 2 ejerce sobre la otra separadas por una distancia r se exprese como:
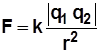
|
Las rayas verticales para q
1
q
2
señalan que se trata de su
valor absoluto
, independiente de su signo (recordemos que el sigo de las cargas (
+ o —)
señala el sentido de la fuerza)
La constante k se expresa como
|
|
Resolvamos algunos problemas aplicando las fórmulas ya conocidas:
Problema 1.-
Dos cargas puntuales (q 1 y q 2 ) se atraen inicialmente entre sí con una fuerza de 600 N , si la separación entre ellas se reduce a un tercio de su valor original ¿cuál es la nueva fuerza de atracción?
Datos
Tenemos que la fórmula de la magnitud de la fuerza eléctrica (F) es
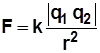
donde
k = constante
q 1 , q 2 = cargas 1 y 2 (Ver: Valor absoluto )
r = distancia entre las cargas
Supongamos que la distancia inicial es "x". Entonces, reemplazando nos queda
![]()
En seguida, llamemos “y” a la fuerza nueva. Ahora la separación es 1/3 de la original, es decir, x/3. Por lo tanto, la nueva fuerza es
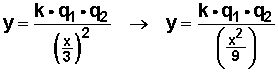
Seguimos operando, invertimos el denominador del segundo miembro y multiplicamos
![]()
Recordemos que
![]()
por lo tanto, si reemplazamos nos queda
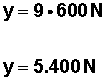
La nueva magnitud de la fuerza es 5.400 N.
Problema 2.-
Una carga de +60 µC (q 1 ) se coloca a 60 mm (r) a la izquierda de una carga de +20 µC (q 2 ) ¿cuál es la fuerza resultante sobre una carga de –35 µC (q 3 ) colocada en el punto medio (r/2) entre las dos cargas?
Datos:
Previamente, los micro coulomb (µC) debemos convertirlos a coulomb (C) y los milímetros (mm) a metros (m) para tener unidades equivalentes para el newton (N) . ( Ver: Notación científica ) .
q 1 = +60 µC = 60 x 10 –6 C (los micro coulomb los expresamos en C)
q 2 = +20 µC = 20 x 10 –6 C (los micro coulomb los expresamos en C)
q 3 = –35 µC = –35 x 10 –6 C (los micro coulomb los expresamos en C)
r = 60 mm = 60 x 10 –3 m (los milímetros los expresamos en metros)
r/2 = 30 mm = 30 x 10 –3 m (los milímetros los expresamos en metros)
Sabemos que la constante es
![]()
Desarrollo
Primero, calculemos la fuerza de atracción entre q 1 y q 3
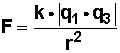
Reemplazamos valores
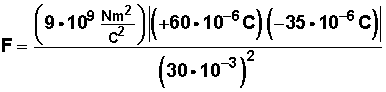
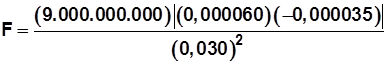
De nuevo: repasar Notación científica
Seguimos. Calculamos
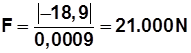
La fuerza entre q 1 y q 3 es de 21.000 N, valor absoluto (se atraen, tienen signos contrarios)
Ahora calculemos la fuerza entre q 2 y q 3
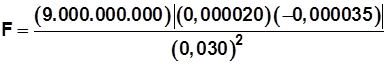
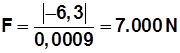
La fuerza entre q 2 y q 3 es de 7.000 N, valor absoluto (se atraen, tienen signos contrarios)
Entonces, como q 3 está sometida a 2 fuerzas que la atraen en distintas direcciones, la fuerza resultante debe ser la diferencia entre ambas; o sea, 21.000 – 7.000 = 14.000 N
Problema 3.-
¿Cuál debe ser la separación entre dos cargas de +5 µC para que la fuerza de repulsión sea 4 N ?
Datos:
q 1 = +5µC = +5 x 10 –6 C
q 2 = +5µC = +5 x 10 –6 C
F = 4 N
k= 9 x 10 9 Nm 2 /C 2
r = x
Usamos la fórmula
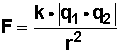
Y en ella reemplazamos los valores:
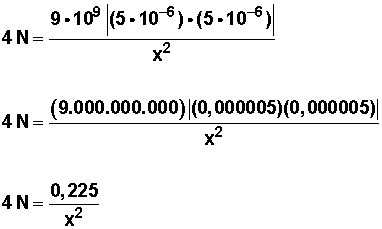
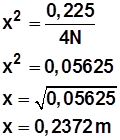
Respuesta:
Para que fuerza de repulsión sea de 4 N las cargas q 1 y q 2 deben estar a 0,2372 metro (237,2 mm).
Problema 4.-
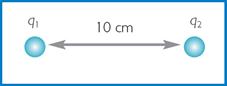
|
Dos cargas desconocidas idénticas ( q 1 y q 2 ) se encuentran sometidas a una fuerza (F) de repulsión de 48 N cuando la distancia (r) entre ellas es de 10 cm ¿cuál es la magnitud de la carga?
¿Te atreves a desarrollarlo solo?
Recuerda: debes convertir los centímetros a metros
Adelante
Volver a: Carga eléctrica
Ver:
http://www.youtube.com/watch?v=64mHVAEBpEY
Ejercicios en:
http://www.youtube.com/watch?v=64mHVAEBpEY
http://www.fisica-facil.com/Temario/Electrostatica/Ejercicios/Ejer-Coulomb1/ejer-colulomb1.htm
http://www.slideshare.net/GONZALOREVELOPABON/ley-de-coulomb-problemas-resueltosgonzalo-revelo-pabon

