Densidad y Volumen |
Densidad es un concepto asociado a la física y el de volumen está asociado a la matemática (geometría).
Una de las tantas características de la física, para hacer descripciones de fenómenos, es hacer mediciones, y las mediciones que se hagan estarán en relación al fenómeno en estudio.
Entre las diversas mediciones que se realizan en física están las que se hacen para obtener el volumen de un cuerpo.

|
| Cuerpos sólidos. |
Volumen
Igual que en geometría, en física suele hablarse de dimensiones, y cuando se habla de dimensiones nos estamos refiriendo a ideas tales como: ancho, largo y alto.
Una dimensión física está relacionada con una línea. Dos dimensiones se relacionan con una superficie. Tres dimensiones se relacionan con un cuerpo.
Los cuerpos , contienen puntos a lo alto, ancho y largo, por lo tanto ocupan un lugar en el espacio .
Por ejemplo: Un libro tiene ancho, largo y alto (que vendría a ser el grosor del libro) y si examinamos bien, veremos que en el interior del libro también hay puntos, hay que darse cuenta que está formado por hojas, una arriba de otra, y que ellas tienen puntos en toda su superficie. Estamos refiriéndonos, con el ejemplo del libro, a un cuerpo sólido.
También hay cuerpos que no son sólidos, por ejemplo una ampolleta; ella ocupa un lugar en el espacio sin embargo en su interior no hay puntos materiales, solo hay puntos geométricos.
El lugar que ocupan los cuerpos en el espacio se denomina volumen. El volumen viene a ser el "tamaño" de un cuerpo.
Hay infinita variedad de cuerpos, por lo que hay infinita variedad de formas volumétricas.
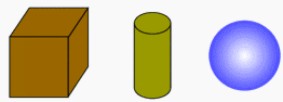
Tal vez las que más nos llaman la atención en su estudio son los paralelepípedos rectangulares (cajas, cubos, cajones, etc.), los cilindros (tubos, alambres, etc.) y las esferas (balones, algunas naranjas, etc.). (Ver: Volúmenes, en Geometría )
|
| Cuerpos de diferentes formas. |
Para medir el volumen de un cuerpo hay diversas fórmulas matemáticas que se relacionan, cada una, con los tipos de cuerpos.
Así, por ejemplo, el volumen de un paralelepípedo de ancho a, largo b y alto c, viene dado por V = abc .
Un cilindro de alto h y radio r tiene un volumen que se calcula con la fórmula V = pr2h .
Una esfera de radio r, tiene un volumen que se calcula con la fórmula
|
|
Tanto el alto como el ancho o el largo de un cuerpo se expresan en unidades de longitud. Así, entonces, la unidad de volumen será de longitud al cubo, por ejemplo el cm3 o el m3 según se utilice el centímetro o el metro para medir cada dimensión respectivamente.
Concluyamos en relación al volumen .
Si examinamos el entorno nuestro veremos muchos cuerpos. Entre ellos hay piedras, troncos, granos de arena, personas, botellas con bebida y botellas vacías, etc., sería interminable la lista. Pero fijémonos en el último ejemplo: botellas con bebida y botellas vacías.
Ambas son cuerpos, porque ocupan una región del espacio; sin embargo, una de ellas tiene materia en su interior, y la otra podría no tenerla. Alguien dirá que si sacamos la bebida quedará aire en su interior. Correcto, pero bien podríamos estar en un ambiente en que no exista aire. En este caso la botella sin bebida no tendría materia en su interior. Sin embargo, la botella sigue siendo botella y sigue ocupando una región del espacio, independiente de que tenga materia en su interior o no la tenga.
Lo anterior es muy importante en el sentido de que hay que tener muy claro que un cuerpo puede ser sólido o no pero sigue ocupando un lugar en el espacio. Y la medida de la región del espacio que ocupa es lo que conocemos por volumen.
Densidad

|
| Plomo puro. |
Se ha observado que un centímetro cúbico (1 cm 3 ) de plomo tiene mayor masa que un centímetro cúbico de aluminio o de un centímetro cúbico de agua. En realidad, se necesitan aproximadamente 4 cm 3 de aluminio y más de 11 cm 3 de agua para equilibrar en la balanza a 1 cm 3 de plomo. Esto demuestra que existen sustancias que son más densas que otras; es decir, tomando volúmenes iguales de diferentes sustancias, se encuentra que algunas tienen más masa que otras.
La densidad de una sustancia o de un material muchas veces caracteriza al material y en el caso de sustancias puras, a menudo sirve para identificar de qué sustancia se trata, pero debe tenerse presente que en algunos casos muy puntuales hay sustancias que tienen la misma densidad o muy parecidas.
Luego, para obtener la densidad de una sustancia, debemos saber su masa y su volumen.
Según esto, se define la densidad como: “ el cociente entre la masa de una muestra de sustancia y el volumen de dicha muestra ”. En forma matemática, esta definición se puede expresar mediante la siguiente fórmula:
|
|
De acuerdo a esto, si se tiene una muestra de una sustancia y se desea determinar su densidad, basta medir su masa a través de una balanza, medir luego el volumen con algún procedimiento adecuado y calcular finalmente el cociente (división) entre la masa y el volumen de la muestra. La densidad quedará expresada en unidades que son el cociente entre las unidades de masa y volumen que se utilizaron en la medición.
Así, por ejemplo, se tiene:
|
|
1 cm 3 = 1 cc = 1 ml |
La densidad del agua es 1.000 kg / m 3 . Todo cuerpo con densidad menor a ésta, flota en el agua (basta que la densidad del cuerpo sea menor que la densidad del agua para que el cuerpo flote). Desde este punto de vista construir un barco de fierro es esencialmente construir un cuerpo de fierro que tenga una densidad menor que la densidad del agua en que debe flotar.

|
| Cuerpo menos denso que el agua. |
Forzosamente el barco debe ser un cuerpo hueco, ya que sólo así el cuociente masa / volumen puede hacerse menor que 1.000 kg / m 3 .
De acuerdo a la expresión matemática, la densidad depende de la cantidad de materia (masa) que se tenga y del volumen que ocupe. Mientras mayor sea la masa del cuerpo, mayor será su densidad y viceversa (son variables directamente proporcionales); mientras mayor sea el volumen que ocupe el cuerpo, menor será su densidad y viceversa (son variables inversamente proporcionales)
Ejemplo 1
¿Qué ocurre con la densidad de una barra de chocolate cuando lo partimos por la mitad?
Respuesta: Nada. El chocolate puede partirse por la mitad, lo que significa que su masa se reduce a la mitad, pero también tiene la mitad del volumen, luego la densidad no cambia.
Densidad de algunas sustancias
|
MATERIAL |
DENSIDAD (g/cm3) |
|
Oro |
19,3 |
|
Plata |
10,5 |
|
Cobre |
8,9 |
|
Hielo |
0,92 |
|
Madera de pino |
0,50 |
Ejemplo 2
Considere una pepita de oro con una masa de 57,9 grs y volumen de 3 cm 3 . Obtenga su densidad.
![]()
La densidad de los sólidos es especialmente importante en la industria de los metales y la industria de los plásticos. Por su parte, la densidad de líquidos es vital en procesos de transporte de fluidos, en el control de calidad de alimentos y en el análisis composición de productos químicos (por ejemplo porcentaje de etanol, contenido de sacarosa en disolución y grados API en derivados del petróleo.
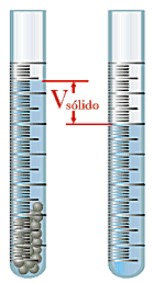
Otro ejemplo práctico
|
Pesar el sólido seco (pequeñas bolitas de acero) en una balanza cuya precisión sea como mínimo de 0,1 g aunque son deseables precisiones de 0,01 g o inferiores
|
|
|
|
|
|
Llenar hasta la mitad con agua el tubo de ensayo graduado y determinar el volumen de líquido introducido. |
|
|
VOLUMEN INICIAL___________ml |
|
|
Introducir el sólido pesado (las bolitas de acero) en el tubo de ensayo graduado.
|
|
|
|
|
|
VOLUMEN FINAL__________ml
|
|
|
Divide la masa del sólido por el volumen que has calculado y averigua en las tablas la naturaleza del sólido cuya densidad has calculado |
|
|
Anota en un cuaderno todas las operaciones que hagas y los resultados que obtengas. |
Ver: Densidad, concepto