PSU: Geometría |
Pregunta 01_2005
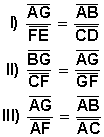
En la figura 1 , si L1 // L2 // L3, entonces ¿cuál(es) de las siguientes afirmaciones es(son) verdadera(s) ?
|
Figura 1 |
Alternativas
A) Sólo I
B) Sólo II
C) Sólo III
D) Sólo I y III
E) I, II y III
Clave: D
Comentario
El contenido que se necesita dominar para resolver este ejercicio es el Teorema de Tales sobre trazos proporcionales, que es un tema que aparece en el programa en Segundo Año de Enseñanza Media.
El alumno debe recordar el teorema de Taales que dice: “Toda paralela a un lado de un triángulo, determina otro triángulo semejante al primero” .
En este caso, se determinan tres triángulos semejantes:
Δ ABG ~ Δ ACF ~ Δ ADE (con el ángulo A común para los tres triángulos).
En la primera afirmación,
![]() se comparan trazos del mismo lado de los triángulos con sus homólogos del otro lado, por lo que es correcta.
se comparan trazos del mismo lado de los triángulos con sus homólogos del otro lado, por lo que es correcta.
En la segunda afirmación,
![]() se compara la paralela menor con la mayor, pero, para ser consecuente, debería compararse el trazo pequeño ( AG ) con el trazo mayor ( AF ) y no con una parte de él (GF ), por lo que es falsa la proporción.
se compara la paralela menor con la mayor, pero, para ser consecuente, debería compararse el trazo pequeño ( AG ) con el trazo mayor ( AF ) y no con una parte de él (GF ), por lo que es falsa la proporción.
En la tercera afirmación,
![]() se compara trazos en el mismo sentido, que corresponde a la comparación más clásica de trazos proporcionales, por lo que es correcta.
se compara trazos en el mismo sentido, que corresponde a la comparación más clásica de trazos proporcionales, por lo que es correcta.
La pregunta resultó medianamente fácil (57 por ciento) para el grupo que contestó el ítem y la omisión no fue tan alta (23 por ciento) si se compara con la omisión de otros ejercicios de geometría. Hay 8 por ciento que consideró sólo II) como correcta y 9 por ciento que se inclinó por las tres afirmaciones como correctas.
Fuente Internet:
Publicación oficial del Demre en www.demre.cl