Vectores en el Plano Cartesiano

Los vectores se definen por tres características, que son: módulo, dirección y sentido . Sabido esto, no es necesario conocer su ubicación en el espacio.

Sin embargo, con la idea de facilitar su estudio resulta más conveniente ubicarlos en un sistema de coordenadas cartesianas , lo cual ayudará a tener mayor precisión al presentarlos tanto de forma algebraica como geométrica.

Una de las opciones más útiles que nos brinda el plano cartesiano es que cuando tenemos un vector que no está en el origen del mismo, lo podemos trasladar, de manera que siempre el origen sea el (0,0) y así facilitar nuestros cálculos, pues sólo necesitaremos el punto final para determinarlo.

Veamos el siguiente dibujo:

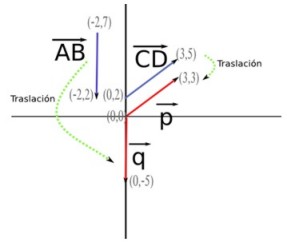
Vector010

Vectores se trasladan al origen.

En el dibujo de arriba, el vector CD (color azul), coordenadas (0, 2) y (3, 5), lo trasladamos (lo bajamos) hasta coordenadas (0, 0) y (3, 3), y lo llamamos vector p (color rojo).

El vector AB (color azul), coordenadas (-2, 7) y (-2, 2), lo trasladamos (lo bajamos y lo corremos hacia el eje y) hasta coordenadas (0, 0) y (0, -5), y lo llamamos vector q .

Utilizando solo el punto final de los vectores trasladados podemos identificarlos:

Vector p = (3, 3)

Vector q = (0, -5)

Nota:

Esta identificación, hecha a partir de las coordenadas del punto final del vector, ahora representa las componentes del vector .

Veamos, entonces ¿qué son o cuáles son las componentes de un vector?

Componentes rectangulares o componentes de un vector

Todo vector se puede escribir o identificar como la suma de otros dos perpendiculares entre sí (ortogonales), puestos en un plano cartesiano. Los vectores que se suman deben estar en alguno de los ejes y sus valores respectivos son las componentes rectangulares del vector resultante.

Las componentes rectangulares se llaman así porque se fundamentan en la construcción de un rectángulo.

Vector011

Dos vectores perpendiculares originan un tercero.

En la imagen de arriba se puede ver que el vector A , no es más que la suma de un vector en el eje "X" (valor 3) y otro en el eje "Y" (valor 6).

A cada uno de estos vectores se le conoce con el nombre de componente, así el vector Ax es la componente "X" (valor 3) del vector A, y el vector Ay es la componente “Y” (valor 6) del mismo vector A; por lo tanto, este vector A = (3, 6).

Ojo: Insistimos: estos valores (3, 6) representan las componentes del vector resultante, no confundir con puntos de coordenadas en un plano (con los cuales pueden ser coincidentes).

Profundicemos en las componentes de un vector.

Para realizar operatoria algebraica con vectores es imprescindible hacerlo usando los valores de sus componentes, por ello resulta tan importante entender y saber cuáles son esas componentes y cómo se reconocen.

En la imagen abajo,el vector v tiene origen en P = (2; 1) y su extremo en Q = (4; 4) .

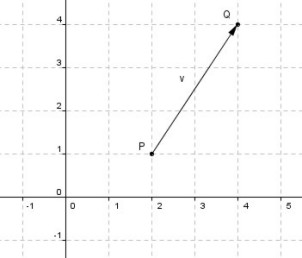
Ojo: Nótese que aquí los pares de dígitos representan cada uno una coordenada en el espacio del plano cartesiano.

Luego, en el gráfico siguiente vemos que vx y vy son las proyecciones del vector sobre los ejes y son las componentes de dicho vector.

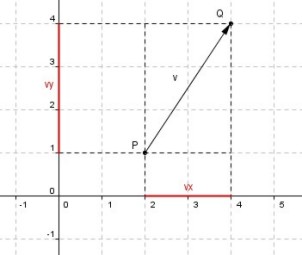
Vector013

Como dato para el futuro próximo, el valor de los componentes será el valor de los catetos del triángulo rectángulo que se puede formar para calcular el valor numérico del vector (que será la hipotenusa).

Entonces, el vector v puede describirse con sus componentes:

De nuevo: No hay que confundir las componentes del vector con las coordenadas de un punto.

Ejemplos de vectores con sus componentes.

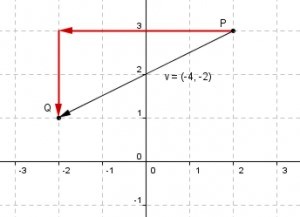
Vector015

V = (–4, –2)

Tenemos el vector v cuyas componentes son –4 y –2

Las componentes de un vector se pueden obtener visualmente trasladando el origen del vector hacia el origen (0, 0) del plano. Pero las componentes del vector también se pueden obtener restando a las coordenadas de su extremo las coordenadas de su origen.

En el ejemplo anterior:

Coordenadas del extremo (–2, 1) menos ( – ) coordenadas del origen (2, 3)

(–2 –2) = –4

(1 – 3) = –2

Veamos otro ejemplo:

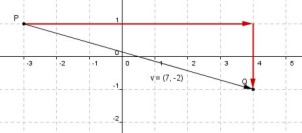
Vector016

V = (7, –2)

Tenemos el vector v cuyas componentes son 7 y –2 .

Hacemos, coordenadas del extremo menos coordenadas del origen:

(4, –1) – (–3, 1)

(4 – –3) = (4 + 3) = 7

(–1 – 1) = –2

Operatoria algebraica de un vector

Calcular el módulo de un vector

Si nos definen un vector por sus componentes, es fácil graficarlo y a la vez calcular su módulo en un plano cartesiano.

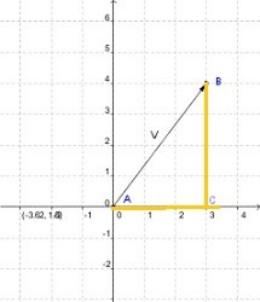
Vector017

Por ejemplo, ¿cuál es el módulo del vector V en la figura arriba?

Veamos:

Sus componentes son V = (3, 4)

Tomemos el triángulo rectángulo ACB (color amarillo) , si V es la hipotenusa y sus catetos valen 3 y 4 unidades, mediante el Teorema de Pitágoras

hipotenusa ² = cateto ² + cateto ²
c ² = a ² + b ²

Entonces:

V ² = 3 ² + 4 ²

V ² = 9 + 16

V ² = 25

V = 5

El vector V vale 5 unidades

Suma y resta algebraica de vectores

Suma algebraica de vectores

Sean dos vectores A y B que se quieren sumar (en la figura), entonces procedemos de la manera gráfica conocida, lo que nos da como resultado el vector R.

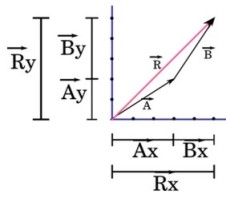
Vector018
Ahora, si escribimos tanto el vector A como el B según sus componentes,

A = (3, 2) y B = (2, 3)

nos damos cuenta de que la suma de las componentes "X" del vector A (es 3) y B (es 2), es la componente "X" (igual a 5) del vector R (3 + 2 = 5)

y que la suma de las componentes “Y” del vector A (es 2) y B (es 3) es la componente "Y" (igual a 5) del mismo vector R (2 + 3 = 5).

Por lo tanto, para sumar vectores algebraicamente, se escribe cada vector según sus componentes y luego se suman las componentes "X" e "Y" de ellos, el resultado será el vector resultante según sus componentes, con las cuales se puede calcular el módulo del vector R.

V _R = (5, 5) según sus componentes

Y podemos calcular su valor (módulo) en unidades

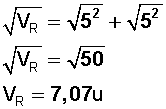
vector021