Antes que todo, debemos recordar que es lo mismo decir inecuaciones que desigualdades.

También se las puede identificar como simultáneas, dobles o de tres partes .

En cualquier caso, se trata de dos o más inecuaciones que tienen soluciones comunes ; esto es, que hay un valor o valores para x que sirven, simultáneamente, para todas.

Encontrar esos valores para x es lo que llamamos “encontrar los límites” o  “encontrar la solución” común para esas inecuaciones.

En los ejercicios sobre esta materia, las inecuaciones pueden presentarse en forma separada o conformando un todo, pero siempre buscando una solución común.

Además, debemos saber que dicha solución puede presentarse en forma desarrollada , como una inecuación, o en forma gráfica , con intervalos.

Antes de continuar, es preciso repasar la materia en:

Ver: Inecuaciones lineales o de primer grado

Ver: Intervalos e inecuaciones lineales

Inecuaciones dobles y separadas

Para entrar en materia con las inecuaciones simultáneas, primero veremos cómo se resuelve un caso con dos inecuaciones presentadas en forma separada:

Veamos un ejemplo:

Ejercicio 1)

Hallar el límite de las soluciones comunes para las inecuaciones

4x – 8 > 8    y   6x + 8 > 14

Primero resolvemos cada inecuación en forma separada:

Primera inecuación: 4x – 8 > 8

4x > 8 + 8 (colocamos a la izquierda los valores con incógnita y a la derecha los números)

Resolvemos

4x > 16

x >16/4

x > 4 (para la primera inecuación, lo cual significa que cualquier número mayor que 4 hasta el infinito es solución)

Entonces x E (4, + ∞) (x pertenece a los naturales desde mayor que 4 (lo cual excluye al 4) hasta el infinito. Recuerden que el paréntesis antes del 4 indica que el 4 está excluido en el intervalo.

Segunda inecuación: 6x + 8 > 14

6x > 14 – 8 (colocamos a la izquierda los valores con incógnita y a la derecha los números).

Resolvemos

6x > 6

x > 6/6

x > 1 (para la segunda inecuación, lo cual significa que cualquier número mayor que 1 hasta el infinito es solución)

Entonces x E (1, + ∞) (x pertenece a los naturales desde mayor que 1 (lo cual excluye al 1) hasta el infinito. Recuerden que el paréntesis antes del 1 indica que el 1 está excluido en el intervalo.

Nuestra solución final para ambas inecuaciones sería

x > 1 > 4  (x mayor que 1, pero mayor que 4); por lo tanto, nuestra solución general es

x > 4  (equis mayor que 4, ya que cualquier  valor mayor que 4  será mayor que 1)

Así, cualquier valor superior a 4 (hasta el infinito) es solución para ambas inecuaciones y 4 es el límite inferior de las soluciones comunes e infinito el límite superior.

Ahora veamos la solución para estas inecuaciones, pero presentadas como intervalo en la recta numérica:

Sabemos, por que ya lo calculamos, que

x  Ε (1, + ∞)   y    x Ε (4, + ∞)

Para la primera x, ponemos un círculo en blanco sobre el 1 y prolongamos una recta hacia la derecha, que llegará hasta el infinito. El círculo sin relleno indica que el 1 queda excluido de las soluciones.

Para la segunda x, ponemos un círculo en blanco sobre el 4 y prolongamos una recta hacia la derecha, que llegará hasta el infinito. El círculo sin relleno indica que el 4 queda excluido de las soluciones.

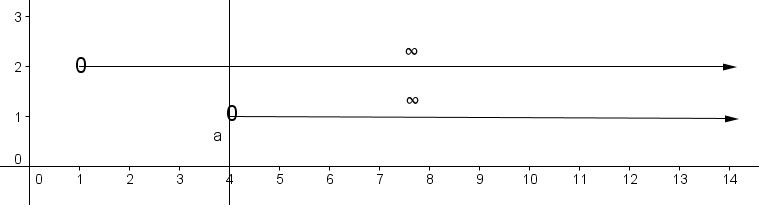
Y la solución general se encuentra a partir de la superposición de los intervalos: desde mayor que 4 (marcado por la raya vertical puesta a modo de guía, pero excluyendo al 4) hasta el infinito.

Respuesta general: x E (4, + ∞) , siendo 4 el límite inferior.

Significa que cualquier número superior al 4 sirve como solución para ambas inecuaciones.

Ejercicio 2)

Hallar el límite de las soluciones comunes de

3x + 4 < 16   y   –6 – x > –8

Primero resolvemos cada inecuación en forma separada:

Primera inecuación: 3x + 4 < 16

3x < 16 – 4

3x < 12

x < 12/3

x < 4  (x menor que 4 para la primera inecuación, lo que excluye al 4).

Segunda inecuación: –6 – x > –8

– x > – 8 + 6

– x > – 2 (amplificamos por –1 para eliminar los negativos, pero debemos cambiar el signo de desigualdad) y queda

x < 2 (x menor que 2 para la segunda inecuación, lo que excluye al 2).

Entonces, x < 2 es la Solución General de ambas inecuaciones, porque todos los valores de “x” menores de 2 son también menores de 4

Por tanto, 2 es el límite superior de las soluciones comunes.

Inecuaciones o desigualdades dobles o de tres partes .

En estos ejemplos, las desigualdades se presentan como un todo, que consta de tres partes.

La incógnita de la desigualdad puede estar solo en el centro o también tanto en el centro como en las partes exteriores.

Para resolver este tipo de inecuaciones simultáneas (de tres partes) necesitamos escribirlas como dos desigualdades separadas y encontrar los valores de “x” que satisfagan a ambas (tal como vimos en el caso anterior).

Inecuación o desigualdad lineal con la incógnita al centro y a un lado .

Veamos el siguiente ejemplo:

–2x + 3 ≤ 4x + 1 < 2x + 9

Lo primero es separar la desigualdad de tres partes para convertirla en dos desigualdades, con un lado en común:

Primera desigualdad: –2x + 3 ≤ 4x + 1

Segunda desigualdad: 4x + 1 < 2x + 9

Y las resolvemos en forma separada:

–2x + 3 ≤ 4x + 1

–2x – 4x ≤ 1 – 3

–6x ≤ –2 (amplificamos por –1, esto cambia los signos, pero debemos cambiar el signo desigualdad)

x ≥ 2/6

x ≥ 1/3  (x igual o mayor a 1/3 es la primera solución)

4x + 1 < 2x + 9

4x – 2x < 9 – 1

2x < 8

x < 8/2

x < 4   (x  menor que 4 es la segunda solución)

Entonces, la respuesta general es que x debe ser igual o mayor que 1/3, pero menor que 4: 1/3 ≤ x < 4

Nuestra respuesta desarrollada podemos obtenerla gráficamente usando intervalos en la recta numérica:

En azul  x ≥ 1/3  (x igual o mayor a 1/3) hasta el infinito positivo (+)

En rojo  x < 4  (x menor que 4) hasta el infinito negativo ( – )

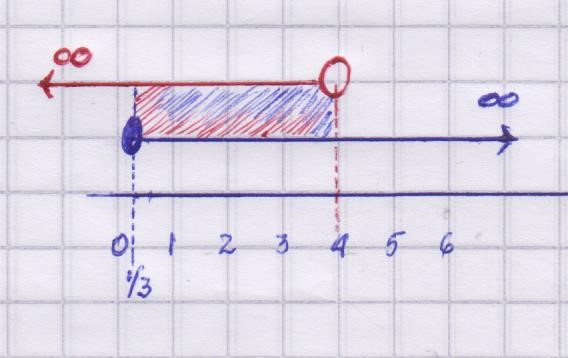
En la figura, la parte común achurada indica la solución:

Que se expresa como: x E [1/3, 4) equis pertenece a los reales desde 1/3 (incluido, lo indica el corchete) hasta 4  (excluido, lo indica el paréntesis)

Volver a: Inecuaciones lineales

Ir a: Ejercicios con Inecuaciones o desigualdades simultáneas